题目内容
16. 如图,反比例函数y=$\frac{k}{x}$的图象与正比例函数y=$\frac{k}{4}$x的图象相交于点A,AB⊥x轴,垂足为B,△ABO的面积=3,求k的值及点A的坐标.
如图,反比例函数y=$\frac{k}{x}$的图象与正比例函数y=$\frac{k}{4}$x的图象相交于点A,AB⊥x轴,垂足为B,△ABO的面积=3,求k的值及点A的坐标.
分析 设A点坐标为(x,y),根据△AOB的面积可求得xy,即可求得k的值,可求得两函数的解析式,解方程组即可得到结果.
解答 解:设A点坐标为(x,y),
则AB=y,OB=-x,
∴S△AOB=$\frac{1}{2}$OB•AB=$\frac{1}{2}$(-x)y=3,
∴k=xy=-6,
∴正比例函数为y=-$\frac{3}{2}$x,反比例函数为y=-$\frac{6}{x}$,
解$\left\{\begin{array}{l}{y=-\frac{2}{3}x}\\{y=-\frac{6}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-3}\\{y=2}\end{array}\right.$,
∵点A在第二象限,
∴点A的坐标(-3,2).
点评 主要考查了反比例函数与一次函数的交点问题,反比例函数y=$\frac{k}{x}$中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得三角形面积为$\frac{1}{2}$|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
19.下列计算不正确的是( )
| A. | -(-3)×$\frac{1}{3}$=-1 | B. | $\frac{4}{5}$+[-(-$\frac{1}{5}$)]=1 | C. | -3+|-3|=0 | D. | -$\frac{1}{5}$÷5=-$\frac{1}{25}$ |
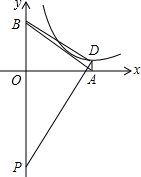 如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+6与x轴、y轴的正半轴分别相交于点A,B两点,点D在反比例函数y=$\frac{k}{x}$(k>0)的图象上,DA⊥OA,点P在y轴负半轴上,OP=14.
如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+6与x轴、y轴的正半轴分别相交于点A,B两点,点D在反比例函数y=$\frac{k}{x}$(k>0)的图象上,DA⊥OA,点P在y轴负半轴上,OP=14.