题目内容
5.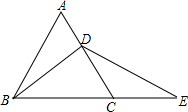 已知△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD=2,连接DE,则DE=2$\sqrt{3}$.
已知△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD=2,连接DE,则DE=2$\sqrt{3}$.
分析 由等边三角形的性质和已知条件得出BD⊥AC,∠DBC=$\frac{1}{2}$∠ABC=30°,由含30°角的直角三角形的性质得出BC=2CD=4,∠E=∠CDE=$\frac{1}{2}$∠BCD=30°,得出∠DBC=∠E,得出DE=DB,由勾股定理即可得出结果.
解答 解:∵△ABC为等边三角形,
∴∠ABC=∠BCD=60°,
∵BD为中线,
∴BD⊥AC,∠DBC=$\frac{1}{2}$∠ABC=30°,
∵CE=CD=2,
∴BC=2CD=4,∠E=∠CDE=$\frac{1}{2}$∠BCD=30°,
∴∠DBC=∠E,
∴DE=DB=$\sqrt{B{C}^{2}-C{D}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$;
故答案为:2$\sqrt{3}$.
点评 本题考查了等边三角形的性质、勾股定理、等腰三角形的判定;熟练掌握等边三角形的性质,证明△BDE为等腰三角形是解决问题的关键.

练习册系列答案
相关题目
17.等腰三角形的两边长分别为4和9,这个三角形的周长是( )
| A. | 17 | B. | 22 | C. | 17或22 | D. | 17和22 |
14.下列各对数中,互为相反数的是( )
| A. | +(-2)与-2 | B. | +(+2)与-2 | C. | -(-2)与2 | D. | 2与+(+2) |
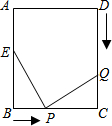 如图,已知长方形ABCD的边长AB=16cm,BC=12cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上由点D向C点运动.则当△BPE与△CQP全等时,P运动时间t为1或3s.
如图,已知长方形ABCD的边长AB=16cm,BC=12cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上由点D向C点运动.则当△BPE与△CQP全等时,P运动时间t为1或3s.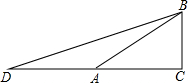 如图所示,在△ABC中,∠C=90°,D是CA延长线上一点,∠BDC=15°,AD=AB=4,则BC=2.
如图所示,在△ABC中,∠C=90°,D是CA延长线上一点,∠BDC=15°,AD=AB=4,则BC=2.
 如图所示,在中国象棋盘上建立一个直角坐标系,设“马”的位置在图中的P点.
如图所示,在中国象棋盘上建立一个直角坐标系,设“马”的位置在图中的P点.