题目内容
1.已知等腰△ABC中,AB=AC=2,腰AB上的高CD与另一腰的夹角为30°,则底边BC的长度为( )| A. | 1或$\sqrt{3}$ | B. | 1或2$\sqrt{3}$ | C. | 2或$\sqrt{3}$ | D. | 2或2$\sqrt{3}$ |
分析 分类讨论:当等腰三角形ABC为锐角三角形,由CD⊥AB,∠ACD=30°,得∠A=60°,证出△ABC是等边三角形,即可得出结果;
当等腰三角形ABC为钝角三角形,由CD⊥AB,∠ACD=30°,得∠DAC=60°,而AB=AC,则∠B=30°,在Rt△BCD中根据含30度的直角三角形三边的关系即可得到BC的长.
解答 解: 当等腰三角形ABC为锐角三角形,如图1,
当等腰三角形ABC为锐角三角形,如图1,
∵CD⊥AB,∠ACD=30°,
∴∠A=60°,
∵AB=AC,
∴△ABC是等边三角形,
∴BC=AB=2;
当等腰三角形ABC为钝角三角形,如图2,
∵CD⊥AB,∠ACD=30°,
∴∠DAC=60°,AD=$\frac{1}{2}$AC=1,
∴CD=$\sqrt{3}$AD=$\sqrt{3}$,
∴BC=2CD=2$\sqrt{3}$;
故选:D.
点评 本题考查了等腰三角形的性质:等腰三角形的两腰相等.也考查了含30度的直角三角形三边的关系以及分类讨论思想的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.小明的哥哥是一名大学生,他利用暑假去一家公司打工,报酬按20元/小时计算,设小明得哥哥这个月的工作时间为t(小时),应得报酬为m(元),请填写下表,然后回答下面问题
(1)你能用含t的代数式表示m的值吗?
(2)在上述问题中,那些是常量?那么是变量?
| 工作时间t(小时) | 1 | 5 | 10 | 15 | 20 | … | t | … |
| 报酬m(元) | 20 | 100 | 200 | 300 | 400 | … | 20t | … |
(2)在上述问题中,那些是常量?那么是变量?
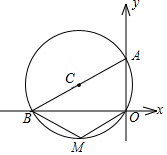 如图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内弧上一点,∠BMO=120°,求⊙C的半径长.
如图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内弧上一点,∠BMO=120°,求⊙C的半径长. 以Rt△ABC的直角顶点C为圆心,作一圆切斜边AB于点T,过点A、B分别作⊙C的切线,E,D为切点,
以Rt△ABC的直角顶点C为圆心,作一圆切斜边AB于点T,过点A、B分别作⊙C的切线,E,D为切点,