题目内容
9.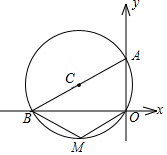 如图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内弧上一点,∠BMO=120°,求⊙C的半径长.
如图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内弧上一点,∠BMO=120°,求⊙C的半径长.
分析 根据圆内接四边形的性质得到∠BAO=60°,根据直角三角形的性质求出AB,计算即可.
解答 解:∵四边形ABMO是圆内接四边形,
∴∠BAO=180°-120°=60°,
∵∠AOB=90°,
∴∠ABO=30°,
∵点A的坐标为(0,3),
∴OA=3,
∴AB=2OA=6,
∴⊙C的半径为3.
点评 本题考查的是圆内接四边形的性质、坐标与图形性质,掌握圆内接四边形的对角互补是解题的关键.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目
14.如果m÷n=12.其中m,n都是正整数,那么它们的最小公倍数是( )
| A. | m | B. | n | C. | 12 | D. | m与n的积 |
1.已知等腰△ABC中,AB=AC=2,腰AB上的高CD与另一腰的夹角为30°,则底边BC的长度为( )
| A. | 1或$\sqrt{3}$ | B. | 1或2$\sqrt{3}$ | C. | 2或$\sqrt{3}$ | D. | 2或2$\sqrt{3}$ |
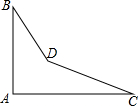 如图,是一个零件的形状,按规定∠A应等于90°,∠B与∠C分别是32°和27°,检测工人量得∠BDC=150°,问该零件是否合格?为什么?
如图,是一个零件的形状,按规定∠A应等于90°,∠B与∠C分别是32°和27°,检测工人量得∠BDC=150°,问该零件是否合格?为什么?