题目内容
10.先化简,($\frac{2a}{a-1}$-$\frac{a}{a+1}$)÷$\frac{1}{{a}^{2}-1}$,再选一个合适的数作为a的值计算.分析 首先把除法转化为乘法,利用分配律计算,然后合并同类项即可化简,然后代入使分式有意义的a的值求解.
解答 解:原式=($\frac{2a}{a-1}$-$\frac{a}{a+1}$)•(a+1)(a-1)
=2a(a+1)-a(a-1)
=2a2+2a-a2+a
=a2+3a.
当a=0时,原式=0.
点评 本题考查分式的化简求值,正确利用分配律计算可以简化计算过程,本题的关键是注意分式有意义的条件,a不等于1和-1.

练习册系列答案
相关题目
1.已知等腰△ABC中,AB=AC=2,腰AB上的高CD与另一腰的夹角为30°,则底边BC的长度为( )
| A. | 1或$\sqrt{3}$ | B. | 1或2$\sqrt{3}$ | C. | 2或$\sqrt{3}$ | D. | 2或2$\sqrt{3}$ |
2. 如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D.则阴影部分面积为(结果保留π)( )
如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D.则阴影部分面积为(结果保留π)( )
 如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D.则阴影部分面积为(结果保留π)( )
如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D.则阴影部分面积为(结果保留π)( )| A. | 24-4π | B. | 32-4π | C. | 32-8π | D. | 24-2π |
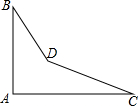 如图,是一个零件的形状,按规定∠A应等于90°,∠B与∠C分别是32°和27°,检测工人量得∠BDC=150°,问该零件是否合格?为什么?
如图,是一个零件的形状,按规定∠A应等于90°,∠B与∠C分别是32°和27°,检测工人量得∠BDC=150°,问该零件是否合格?为什么? 如图,在平面直角坐标系中,A(2,2),B(-1,0),C (3,0)
如图,在平面直角坐标系中,A(2,2),B(-1,0),C (3,0)