题目内容
11.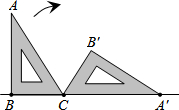 如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置,若BC的长为1cm,求点A从开始到结束经过的路径长.
如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置,若BC的长为1cm,求点A从开始到结束经过的路径长.
分析 根据含30度的直角三角形三边的关系得到AC=2BC=30,且∠ACB=60°,再根据旋转的性质得到∠ACA′=120°,则顶点A从开始到结束所经过的路径为弧AA′,然后根据弧长公式计算即可.
解答 解:∵∠A=30°,∠ABC=90°,BC=1,
∴AC=2BC=2,∠ACB=60°,
∵直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置,
∴∠ACA′=180°-60°=120°,
∴顶点A从开始到结束所经过的路径长=$\frac{120•π•2}{180}$=$\frac{4}{3}$π(cm).
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.旋转三要素:旋转中心; 旋转方向; 旋转角度.也考查了弧长公式.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
1.为了更好治理闽江水质,保护环境,市治污公司决定购买10台污水处理设备.现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:
经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备和3台B型设备共49万元.
(1)求a,b的值.
(2)经预算:市治污公司购买污水处理设备的资金不超过106万元,且该月要求处理闽江的污水量不低于2240吨,你认为该公司有哪几种购买方案,分别为哪几种?
(3)在(2)的条件下,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
| A型 | B型 | |
| 价格(万元/台) | a | b |
| 处理污水量(吨/月) | 240 | 200 |
(1)求a,b的值.
(2)经预算:市治污公司购买污水处理设备的资金不超过106万元,且该月要求处理闽江的污水量不低于2240吨,你认为该公司有哪几种购买方案,分别为哪几种?
(3)在(2)的条件下,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
1.4个红球、6个白球放入一个不透明的盒子里,从中任摸出5个球,恰好红球、白球都摸到,这个事件是( )
| A. | 必然事件 | B. | 不可能发生 | C. | 可能发生 | D. | 很可能发生 |
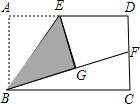 如图,在矩形纸片ABCD的边AD上取中点E,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,将BG延长交DC于点F,若DF=CF,则$\frac{AD}{AB}$的值$\sqrt{2}$.
如图,在矩形纸片ABCD的边AD上取中点E,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,将BG延长交DC于点F,若DF=CF,则$\frac{AD}{AB}$的值$\sqrt{2}$.
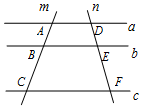 如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若$\frac{AB}{BC}=\frac{1}{2}$,则$\frac{DE}{DF}$=$\frac{1}{3}$.
如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若$\frac{AB}{BC}=\frac{1}{2}$,则$\frac{DE}{DF}$=$\frac{1}{3}$.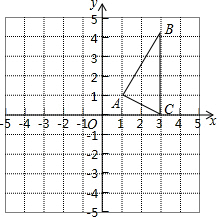 在平面直角坐标系中,△ABC的三个顶点坐标分别为(1,1)、(3,4)、(3,0).
在平面直角坐标系中,△ABC的三个顶点坐标分别为(1,1)、(3,4)、(3,0).