题目内容
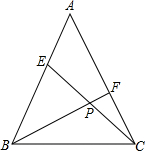等腰△ABC中，AB=AC，E、F分别是AB、AC上的点，且BE=AF，连接CE、BF交于点P．若| CP |
| PE |
| 3 |
| 4 |
| AE |
| AF |
考点：平行线分线段成比例,等腰三角形的性质
专题：计算题
分析：作ED∥AC交BF于D，如图，根据平行于三角形的一边，并且和其他两边（或两边的延长线）相交的直线，所截得的三角形的三边与原三角形的三边对应成比例得到
=
=
，设ED=4x，BE=y，则FC=3x，AF=y，易得AE=FC=3x，再利用DE∥AF得到
=
，即
=
，利用比例的性质和解方程得到y=6x，然后计算
的值．
| ED |
| FC |
| EP |
| PC |
| 4 |
| 3 |
| BE |
| BA |
| DE |
| AF |
| y |
| y+3x |
| 4x |
| y |
| AE |
| AF |
解答：解：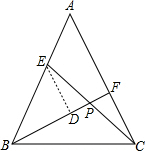
作ED∥AC交BF于D，如图，
∵ED∥FC，
∴
=
=
，
设ED=4x，BE=y，则FC=3x，AF=y，
∵AB=AC，
∴AE=FC=3x，
∵DE∥AF，
∴
=
，即
=
，
整理得y2-4xy+12x2=0，
∴（y+2x）（y-6x）=0，
∴y=6x，
∴
=
=
．
故答案为
．
作ED∥AC交BF于D，如图，∵ED∥FC，
∴
| ED |
| FC |
| EP |
| PC |
| 4 |
| 3 |
设ED=4x，BE=y，则FC=3x，AF=y，
∵AB=AC，
∴AE=FC=3x，
∵DE∥AF，
∴
| BE |
| BA |
| DE |
| AF |
| y |
| y+3x |
| 4x |
| y |
整理得y2-4xy+12x2=0，
∴（y+2x）（y-6x）=0，
∴y=6x，
∴
| AE |
| AF |
| 3x |
| 6x |
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
点评：本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例；平行于三角形的一边，并且和其他两边（或两边的延长线）相交的直线，所截得的三角形的三边与原三角形的三边对应成比例．也考查了等腰三角形的性质．
练习册系列答案
阅读快车系列答案
相关题目
已知二次函数y=ax2+bx+c的图象如图所示，其对称轴为直线x=-1，给出下列结论：（1）b2＞4ac； （2）abc＞0；（3）2a+b=0；（4）a+b+c＞0；（5）a-b+c＜0．其中正确的结论有（ ）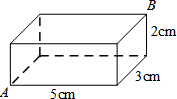
如图，已知长方体的长、宽、高分别是5cm、3cm、2cm，一只蚂蚁要从长方体盒子的一个顶点A处，沿着长方体的表面到长方体和A相对的顶点B处吃食物，那么它需要爬行的最短路径的长是
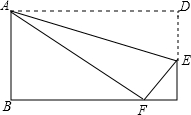如图，矩形ABCD边上AD沿折痕AE折叠，使点D落在BC上的F处，已知AB=6，△ABF的面积是24，求FE的长．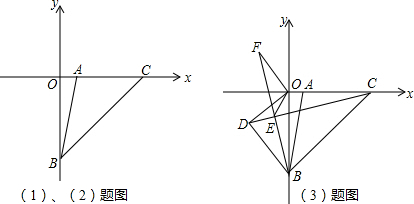
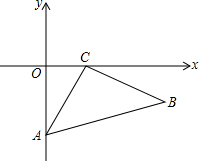已知：在平面直角坐标系中，△ABC的顶点A、C分别在y轴、x轴上，且∠ACB=90°，AC=BC．如图，当A（0，-2），C（1，0），点B在第四象限时，则点B的坐标为：（