题目内容
20.三角形的两边长分别是3和4,请写出一个无理数表示第三边的长,这个数可以是$\sqrt{5}$.分析 先根据三角形三边关系求得第三边的范围,再根据第三边为无理数,求得第三边即可.
解答 解:∵三角形的两边长分别是3和4,
∴1<第三边<7,
又∵第三边为无理数,
∴第三边可以为$\sqrt{5}$等.
故答案为:$\sqrt{5}$
点评 本题主要考查了三角形的三边关系,解决问题的关键是根据第三边的范围求得第三边的长.注意无理数有三种常见的形式:①开方开不尽的数,②无限不循环小数,③含有π的数.

练习册系列答案
相关题目
12.下列各式中,同学们的计算结果不正确的是( )
| A. | $\sqrt{5}×\sqrt{7}$=2$\sqrt{3}$ | B. | $\sqrt{6}÷\sqrt{3}$=$\sqrt{2}$ | C. | $\sqrt{\frac{1}{10}}$×$\sqrt{8}$=$\frac{2\sqrt{5}}{5}$ | D. | $\sqrt{\frac{4}{7}}$÷$\sqrt{\frac{7}{4}}$=$\frac{4}{7}$ |
16.甲、乙两人做同样的零件,如果甲先做1天,乙再开始做,5天后两人做的一样多,如果甲先做30个,乙再开始做,4天后乙反比甲多做10个.甲,乙两人每天分别做多少个?设甲,每天做x个,乙每天做y个,列出的方程组是( )
| A. | $\left\{\begin{array}{l}{6x=5y}\\{30+4x=4y+10}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{1+5x=6y}\\{30+4x=4y-10}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{6x=5y}\\{30+4x=4y-10}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{1+5x=5y}\\{30+4x=4y+10}\end{array}\right.$ |
8.下列说法正确的是( )
| A. | 0的立方根是0.2 | B. | 4的平方根是±4 | C. | -1的立方根是-1 | D. | -25没有立方根 |
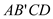 沿对角形线AC折叠,得到如图所示的图形,已知∠BAO=30°,
沿对角形线AC折叠,得到如图所示的图形,已知∠BAO=30°,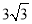 ,OD=
,OD=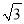 ,求CD的长
,求CD的长