题目内容
2.平行四边形ABCD中一个角的平分线把一条边分成3cm和4cm两部分,则这个四边形的周长是20或22cm.分析 利用平行四边形的性质和角平分线证出∠DAE=∠BEA,得出AB=BE,由此求出另一边,从而求出周长,注意两种情况.
解答 解:如图所示: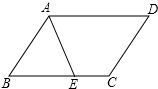
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AD∥BC,
∵∠A的平分线交BC于点E,
∴∠BAE=∠DAE
∵AD∥BC,
∴∠DEA=∠BEA,
∴∠DAE=∠BEA
∴AB=BE,
分两种情况进行讨论:
当BE=3cm,EC=4cm时,AB=BE=3cm,BC=7cm,平行四边形的周长=2(3+7)=20(cm);
当BE=4cm,EC=3cm时,AB=BE=4cm,BC=7cm,平行四边形的周长=2(4+7)=22(cm);
综上所述:?ABCD的周长是22或22cm.
故答案为20或22.
点评 本题考查了平行四边形的性质、等腰三角形的判定;熟练掌握平行四边形的性质,证明AB=BE是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.如果线段a,b,c能组成直角三角形,则它们的比可以是( )
| A. | 1:2:4 | B. | 1:3:5 | C. | 6:4:7 | D. | 5:12:13 |
7.若-1是关于x的方程nx2+mx+2=0(n≠0)的一个根,则m-n的值为( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
14.某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总数排列名次,在一分钟内踢100个以上(含100个)为优秀.如表是成绩最好的甲、乙两班各5名学生的比赛数据.(单位:个)
经统计发现甲、乙两班总个数相同,方差分别为46.8,103.2(平方个).试从中位数,方差,优秀率三个方面考虑,哪个班为冠军?
| 1号 | 2号 | 3号 | 4号 | 5号 | 总个数 | |
| 甲班 | 89 | 100 | 98 | 110 | 103 | 500 |
| 乙班 | 100 | 89 | 97 | 119 | 95 | 500 |
 甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图象如图所示.
甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图象如图所示. 如图所示,口袋中有5张完全相同的卡片,分别写有1cm,2cm,3cm,4cm和5cm,口袋外有两张卡片,分别写有4cm和5cm.现随机从袋内取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,按要求回答下列问题:
如图所示,口袋中有5张完全相同的卡片,分别写有1cm,2cm,3cm,4cm和5cm,口袋外有两张卡片,分别写有4cm和5cm.现随机从袋内取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,按要求回答下列问题: