题目内容
10.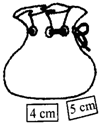 如图所示,口袋中有5张完全相同的卡片,分别写有1cm,2cm,3cm,4cm和5cm,口袋外有两张卡片,分别写有4cm和5cm.现随机从袋内取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,按要求回答下列问题:
如图所示,口袋中有5张完全相同的卡片,分别写有1cm,2cm,3cm,4cm和5cm,口袋外有两张卡片,分别写有4cm和5cm.现随机从袋内取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,按要求回答下列问题:(1)求这三条线段能构成三角形的概率;
(2)求这三条线段能构成等腰三角形的概率.
分析 (1)根据题意可以写出所有的可能性,根据三角形两边之和大于第三边可以判断有几种可能性符合要求,从而可以求得这三条线段能构成三角形的概率;
(2)根据等腰三角形的定义可以得到哪几组符号要求,从而可以得到这三条线段能构成等腰三角形的概率.
解答 解:(1)由题意可得,
随机从袋内取出一张卡片,与口袋外两张卡片放在一起的所有可能性是:
(1、4、5),(2、4、5),(3、4、5),(4、4、5),(5、4、5),
∵1+4=5,则(1、4、5)这组不能构成三角形,
∴这三条线段能构成三角形的概率是$\frac{4}{5}$;
(2)由题意可得(4、4、5),(5、4、5)这两组可以构成等腰三角形,
∴这三条线段能构成等腰三角形的概率是$\frac{2}{5}$.
点评 本题考查列表法与树状图法、三角形的三边关系、等腰三角形的判定,解题的关键是明确题意,可以写出所有的可能性,求出相应的概率.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
1.下列直角坐标系中,不能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
18.随着人们环保意识的增强,PM2.5成为2012年人们关注的热词.PM2.5是指粒径小于2.5微米即(0.0025毫米)的颗粒物,它悬浮在空中,能进入人体呼吸道,危害健康,将0.0025用科学记数可表示为( )
| A. | 0.25×10-2 | B. | 2.5×10-3 | C. | 2.5×10-2 | D. | 2.5×104 |
15.“五一”期间,某中学数学兴趣小组的同学们租一辆小型巴士前去某地进行社会实践活动,租车租价为180元.出发时又增加了两位同学,结果每位同学比原来少分摊了3元车费.若小组原有x人,则所列方程为( )
| A. | $\frac{180}{x}$-$\frac{180}{x-2}$=3 | B. | $\frac{180}{x}$-$\frac{180}{x+2}$=3 | C. | $\frac{180}{x+2}$-$\frac{180}{x}$=3 | D. | $\frac{180}{x-2}$-$\frac{180}{x}$=3 |
19.下列计算错误的是( )
| A. | 2m+3n=5mn | B. | a6÷a2=a4 | C. | (a2)3=a6 | D. | a•a2=a3 |
 一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.