题目内容
4.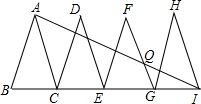 如图,已知△ABC、△DCE、△FEG、△HGI是4个全等的等腰三角形,底边BC、CE、EG、GI在同一直线上,且AB=2,BC=1,连接AI,交FG于点Q,则QI=$\frac{4}{3}$.
如图,已知△ABC、△DCE、△FEG、△HGI是4个全等的等腰三角形,底边BC、CE、EG、GI在同一直线上,且AB=2,BC=1,连接AI,交FG于点Q,则QI=$\frac{4}{3}$.
分析 由题意得出BC=1,BI=4,则$\frac{AB}{BI}$=$\frac{BC}{AB}$,再由∠ABI=∠ABC,得△ABI∽△CBA,根据相似三角形的性质得$\frac{AC}{AI}$=$\frac{AB}{BI}$,求出AI,根据全等三角形性质得到∠ACB=∠FGE,于是得到AC∥FG,得到比例式$\frac{QI}{AI}$=$\frac{GI}{CI}$=$\frac{1}{3}$,即可得到结果.
解答 解:∵△ABC、△DCE、△FEG是三个全等的等腰三角形,
∴HI=AB=2,GI=BC=1,BI=4BC=4,
∴$\frac{AB}{BI}$=$\frac{2}{4}$=$\frac{1}{2}$,$\frac{BC}{AB}$=$\frac{1}{2}$,
∴$\frac{AB}{BI}$=$\frac{BC}{AB}$,
∵∠ABI=∠ABC,
∴△ABI∽△CBA;
∴$\frac{AC}{AI}$=$\frac{AB}{BI}$,
∵AB=AC,
∴AI=BI=4;
∵∠ACB=∠FGE,
∴AC∥FG,
∴$\frac{QI}{AI}$=$\frac{GI}{CI}$=$\frac{1}{3}$,
∴QI=$\frac{1}{3}$AI=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题主要考查了平行线分线段定理,以及三角形相似的判定,正确理解AB∥CD∥EF,AC∥DE∥FG是解题的关键.

练习册系列答案
相关题目
19.下列方程的变形正确的是( )
| A. | 由3+x=5,得x=5+3 | B. | 由7x=-3,得x=-$\frac{7}{3}$ | C. | 由2y=0,得y=$\frac{1}{2}$ | D. | 由-2x-6=0得x=-3 |
9.北京在2015年6月初申办2022冬季奥运会的陈述中表示,若申办成功,这项活动将带动的3.2亿人参与,将3.2亿用科学记数法表示为( )
| A. | 32×107 | B. | 3.2×108 | C. | 3.2×109 | D. | 0.32×1010 |
16.若$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$是方程组$\left\{\begin{array}{l}{ax+by=0}\\{3ax-2by=2}\end{array}\right.$的解,则下列等式成立的是( )
| A. | a+2b=0 | B. | a+b=0 | C. | a-2b=0 | D. | a-b=0 |
13.下列式子错误的是( )
| A. | -$\sqrt{0.04}$=-0.2 | B. | $\root{3}{0.001}$=0.1 | C. | $\root{3}{(-5)^{3}}$=-5 | D. | $\sqrt{81}$=±9 |