题目内容
11.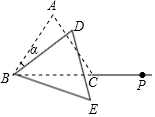 如图,等边三角形ABC中,AB=5,延长BC至点P,使CP=3,将△ABC绕点B顺时针旋转a角(0<a<60°),得到△DBE,连接DP、EP,则当△DPE为等腰三角形时,点D到直线BP的距离为3或$\frac{5}{2}$或$\frac{4\sqrt{3}-3}{5}$.
如图,等边三角形ABC中,AB=5,延长BC至点P,使CP=3,将△ABC绕点B顺时针旋转a角(0<a<60°),得到△DBE,连接DP、EP,则当△DPE为等腰三角形时,点D到直线BP的距离为3或$\frac{5}{2}$或$\frac{4\sqrt{3}-3}{5}$.
分析 当△DPE为等腰三角形时,分三种情形①当PD=DE=5时,则BD=DP,如图1,过D作DF⊥PB于F.②当PE=DE=5时,如图2,作PM⊥BD交BD的延长线于M.作EF⊥PB于F.作DG⊥PB于G.③当PD=PE=5时,如图3,分别构建方程求解即可.
解答  解:∵在等边三角形ABC中,AB=5,
解:∵在等边三角形ABC中,AB=5,
∴BC=AB=5,
∴BP=8,
∵将△ABC绕点B顺时针旋转a角(0<a<60°),得到△DBE,
∴BD=DE=BE=5,
当△DPE为等腰三角形时,
①当PD=DE=5时,则BD=DP,如图1,过D作DF⊥PB于F,则BF=PF=$\frac{1}{2}$BP=4,
∴DF=$\sqrt{D{P}^{2}-P{F}^{2}}$=3,
∴点D到直线BP的距离为3;
②当PE=DE=5时,如图2,作PM⊥BD交BD的延长线于M.作EF⊥PB于F.作DG⊥PB于G.
∵EB=ED=EP,
∴∠BDE+$\frac{1}{2}$∠BED=90°,∠EDP+$\frac{1}{2}$∠DEP=90°,
∴∠BDE+∠EDP+$\frac{1}{2}$∠BEP=180°,
∵∠BDP+∠PDM=180°,
∴∠PDM=$\frac{1}{2}$∠BEP=∠BEF,
∴tan∠PDM=tan∠BEF=$\frac{4}{3}$=$\frac{PM}{DM}$,设PM=4k,DM=3k,
在Rt△MPB中,∵BM2+PM2=PB2,
∴(5+3k)2+(4k)2=82,
解得k=$\frac{-3+4\sqrt{3}}{5}$或$\frac{-3-4\sqrt{3}}{5}$(舍弃),
∵$\frac{1}{2}$•BD•PM=$\frac{1}{2}$•PB•DG,
∴5×$\frac{-12+16\sqrt{3}}{5}$=8×DG,
∴DG=$\frac{4\sqrt{3}-3}{2}$
③当PD=PE=5时,如图3,
由旋转知,BD=BE=DE=5,∵PB=PB,
∴△DBP≌△EBP,
∴∠DBP=∠EBP,
∵BD=BE,
∴BP⊥DE,
EF=$\frac{1}{2}$DE=$\frac{5}{2}$;
综上所述,点D到直线BP的距离为3或$\frac{5}{2}$或$\frac{4\sqrt{3}-3}{5}$.
故答案为3或$\frac{5}{2}$或$\frac{4\sqrt{3}-3}{5}$.
点评 本题考查旋转变换、等边三角形的性质,解直角三角形等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考填空题中的压轴题.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案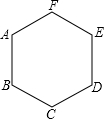 如图,已知正六边形ABCDEF的边长为5cm,一只电子蚂蚁从顶点A出发沿着正六边形的边爬行,当爬行50cm时,电子蚂蚁离A点的距离为 ( )
如图,已知正六边形ABCDEF的边长为5cm,一只电子蚂蚁从顶点A出发沿着正六边形的边爬行,当爬行50cm时,电子蚂蚁离A点的距离为 ( )| A. | $5\sqrt{2}$cm | B. | $5{\sqrt{3}^{\;}}$cm | C. | 5(1+$\sqrt{2}$)cm | D. | 5(1+$\sqrt{3}$)cm |
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | 5 | D. | -5 |
| A. | (-2017)2 | B. | -(-2017) | C. | -|-2017| | D. | 2017-2 |
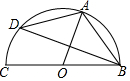 如图A,D是⊙O上两点,BC是直径.若∠D=35°,则∠OAB的度数是( )
如图A,D是⊙O上两点,BC是直径.若∠D=35°,则∠OAB的度数是( )| A. | 35° | B. | 55° | C. | 65° | D. | 70° |
 如图,E是线段AD上一点,AB=AC,BE=CE,求证:
如图,E是线段AD上一点,AB=AC,BE=CE,求证: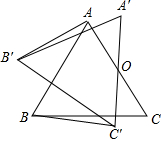 已知:如图,等边三角形△ABC,O为AC边的中点,将△ABC绕点O顺时针旋转α角(0°<α<90°)到△A′B′C′的位置,连接AB′,BC′.
已知:如图,等边三角形△ABC,O为AC边的中点,将△ABC绕点O顺时针旋转α角(0°<α<90°)到△A′B′C′的位置,连接AB′,BC′.