题目内容
某人在路边摆摊“幸运6+1”的游戏,他在一只黑色袋子内装有形状、大小、质地都一样的球7个,其中红色球1个,白球6个,白球分别编号为1-6号,摸奖规则为:交一元钱可摸奖一次,每次从口袋中摸出一个球,摸球前自己先确定一个1-6内的数为中奖号,如果摸中号码与你确定号码一样的白球,获奖4元,如果摸出红球,奖2元.
(1)计算中奖的概率;
(2)小陈同学原有20元钱,参加“摸奖”4次后,手中共有26元钱,设小陈抽中红球x次,抽中白球确定号码一样的次数有y次,试确定x和y的值;
(3)小陈因此认为把手中的钱都用来“摸奖”,一定可以赢取更多的钱,你认为他的想法对吗?为什么?
(1)计算中奖的概率;
(2)小陈同学原有20元钱,参加“摸奖”4次后,手中共有26元钱,设小陈抽中红球x次,抽中白球确定号码一样的次数有y次,试确定x和y的值;
(3)小陈因此认为把手中的钱都用来“摸奖”,一定可以赢取更多的钱,你认为他的想法对吗?为什么?
考点:概率公式
专题:计算题
分析:(1)利用概率公式计算;
(2)抽中红球x次,得2x元,抽中白球确定号码一样的次数有y次,得4y元,则2x+4y-4=26-20,然后通过讨论二元一次方程的特殊解得到满足条件的x和y的值;
(3)利用中奖是随机事件进行回答.
(2)抽中红球x次,得2x元,抽中白球确定号码一样的次数有y次,得4y元,则2x+4y-4=26-20,然后通过讨论二元一次方程的特殊解得到满足条件的x和y的值;
(3)利用中奖是随机事件进行回答.
解答:解:(1)中奖的概率=
;
(2)根据题意得2x+4y-4=26-20,
则x+2y=5,
当y=0时,x=5;当y=1时,x=3;当y=2时,x=1,
而x+y≤4,
所以x=3,y=1;当x=1时,y=2;
(3)他的想法不对.因为中奖是随机事件,中奖的概率为
.
| 2 |
| 7 |
(2)根据题意得2x+4y-4=26-20,
则x+2y=5,
当y=0时,x=5;当y=1时,x=3;当y=2时,x=1,
而x+y≤4,
所以x=3,y=1;当x=1时,y=2;
(3)他的想法不对.因为中奖是随机事件,中奖的概率为
| 2 |
| 7 |
点评:本题考查了概率公式:随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.P(必然事件)=1.P(不可能事件)=0.

练习册系列答案
相关题目
在以下四个图形中,不是轴对称图形的是( )
| A、锐角 | B、等腰三角形 |
| C、平行四边形 | D、长方形 |
有一人患了流感,经过两轮传染后共有64人患了流感.则每轮传染中平均一个人传染了几个人?( )
| A、10人 | B、6人 | C、7人 | D、8人 |
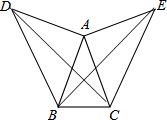 如图所示,在△ABC中,AB=AC,∠BAC=42°,F分别以AB,AC为边,作两个等腰直角△ADB和△ACE,使得∠BAD=∠CAE=90°,连接BE,CD.
如图所示,在△ABC中,AB=AC,∠BAC=42°,F分别以AB,AC为边,作两个等腰直角△ADB和△ACE,使得∠BAD=∠CAE=90°,连接BE,CD. 如图所示,直线AB,CD交点于O,OE平分∠BOD,且∠3:∠2=8:1,求∠AOC的度数.
如图所示,直线AB,CD交点于O,OE平分∠BOD,且∠3:∠2=8:1,求∠AOC的度数.