题目内容
已知直线l上有一点O,点A、B同时从O出发,在直线l上分别向左、向右作匀速运动,且A、B的速度比为1:2,设运动时间为ts.
(1)当t=2s时,AB=12cm.此时,
①在直线l上画出A、B两点运动2秒时的位置,并回答点A运动的速度是 cm/s; 点B运动的速度是 cm/s.
②若点P为直线l上一点,且PA-PB=OP,求OP、AB的值;
(2)在(1)的条件下,若A、B同时按原速向左运动,再经过几秒,OA=2OB?
(3)在(1)的条件下,都往左运动,经过几秒A、O、B三点中一点会成为其他两点的中点?
(1)当t=2s时,AB=12cm.此时,
①在直线l上画出A、B两点运动2秒时的位置,并回答点A运动的速度是
②若点P为直线l上一点,且PA-PB=OP,求OP、AB的值;
(2)在(1)的条件下,若A、B同时按原速向左运动,再经过几秒,OA=2OB?
(3)在(1)的条件下,都往左运动,经过几秒A、O、B三点中一点会成为其他两点的中点?
考点:一元一次方程的应用,两点间的距离
专题:
分析:(1)①设A的速度为xcm/s,B的速度为2xcm/s,根据2s相距的距离为12建立方程求出其解即可;
②分情况讨论如图2,如图3,建立方程求出OP的值就可以求出结论;
(2)设A、B同时按原速向左运动,再经过几a秒OA=2OB,根据追击问题的数量关系建立方程求出其解即可;
(3)设A、B同时按原速向左运动,再经过a秒A,O,B三点中一点会成为其他两点的中点,分类列方程解决问题.
②分情况讨论如图2,如图3,建立方程求出OP的值就可以求出结论;
(2)设A、B同时按原速向左运动,再经过几a秒OA=2OB,根据追击问题的数量关系建立方程求出其解即可;
(3)设A、B同时按原速向左运动,再经过a秒A,O,B三点中一点会成为其他两点的中点,分类列方程解决问题.
解答:解:(1)①设A的速度为xcm/s,B的速度为2xcm/s,由题意,得
2x+4x=12,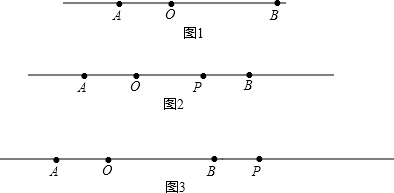
解得:x=2,
∴B的速度为4cm/s;
故答案为:2,4.
②如图2,当P在AB之间时,
∵PA-OA=OP,PA-PB=OP,
∴PA-OA=PA-PB,
∴OA=PB=4,
∴OP=4.
∴AB=12.
如图3,当P在AB的右侧时,
∵PA-OA=OP,PA-PB=OP,
∴PA-OA=PA-PB,
∴OA=PB=4,
∴OP=12.
∴AB=12;
(2)设A、B同时按原速向左运动,再经过几a秒OA=2OB,由题意,得
2a+4=2(8-4a)或2a+4=2(4a-8),
解得:a=
或a=
.
答:再经过
或
秒时OA=2OB.
(3)设A、B同时按原速向左运动,再经过a秒A,O,B三点中一点会成为其他两点的中点,
由题意,得
2a+4=(8-4a)或2a+4=2(4a-8)或4a-8=2(2a+4),
解得:a=
或a=
或无解.
答:再经过
或1
秒A,O,B三点中一点会成为其他两点的中点.
2x+4x=12,

解得:x=2,
∴B的速度为4cm/s;
故答案为:2,4.
②如图2,当P在AB之间时,
∵PA-OA=OP,PA-PB=OP,
∴PA-OA=PA-PB,
∴OA=PB=4,
∴OP=4.
∴AB=12.
如图3,当P在AB的右侧时,
∵PA-OA=OP,PA-PB=OP,
∴PA-OA=PA-PB,
∴OA=PB=4,
∴OP=12.
∴AB=12;
(2)设A、B同时按原速向左运动,再经过几a秒OA=2OB,由题意,得
2a+4=2(8-4a)或2a+4=2(4a-8),
解得:a=
| 6 |
| 5 |
| 10 |
| 3 |
答:再经过
| 6 |
| 5 |
| 10 |
| 3 |
(3)设A、B同时按原速向左运动,再经过a秒A,O,B三点中一点会成为其他两点的中点,
由题意,得
2a+4=(8-4a)或2a+4=2(4a-8)或4a-8=2(2a+4),
解得:a=
| 2 |
| 3 |
| 10 |
| 3 |
答:再经过
| 2 |
| 3 |
| 10 |
| 3 |
点评:本题考查一元一次方程解实际问题的运用,追击问题的数量关系的运用,解答时由行程问题的数量关系建立方程是关键.

练习册系列答案
相关题目

 把一根长16米的钢管截成12段,再焊接成一个长方体形状的架子(如图所示),若要求高与宽都是1米,那么做成这个长方体形状的架子体积有多大?
把一根长16米的钢管截成12段,再焊接成一个长方体形状的架子(如图所示),若要求高与宽都是1米,那么做成这个长方体形状的架子体积有多大? 若a、b、c三个数在数轴上的位置如图所示,化简|a-b|-|b-c|+|c+a|+|b|-2|a|.
若a、b、c三个数在数轴上的位置如图所示,化简|a-b|-|b-c|+|c+a|+|b|-2|a|. 如图是由五个边长为1的小正方形组成的十字形.
如图是由五个边长为1的小正方形组成的十字形.