题目内容
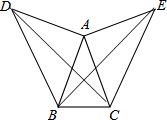 如图所示,在△ABC中,AB=AC,∠BAC=42°,F分别以AB,AC为边,作两个等腰直角△ADB和△ACE,使得∠BAD=∠CAE=90°,连接BE,CD.
如图所示,在△ABC中,AB=AC,∠BAC=42°,F分别以AB,AC为边,作两个等腰直角△ADB和△ACE,使得∠BAD=∠CAE=90°,连接BE,CD.(1)求∠DBC的度数;
(2)求证:BE=CD.
考点:全等三角形的判定与性质
专题:
分析:(1)易求得∠ABC的度数和∠DBA=45°,即可解题;
(2)易证∠DBC=∠ECB,BD=CE,即可证明△DBC≌△ECB,可得BE=CD,即可解题.
(2)易证∠DBC=∠ECB,BD=CE,即可证明△DBC≌△ECB,可得BE=CD,即可解题.
解答:(1)解:∵AB=AC,∠BAC=42°,
∴∠ABC=∠ACB=69°,
∵△ADB是等腰直角三角形,
∴∠DBA=45°,
∴∠DBC=∠DBA+∠ABC=114°;
(2)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵△ADB、△ACE是等腰直角三角形,
∴∠DBA=∠ECA=45°,
∴∠DBC=∠ECB,
∵AB=AC,BD=
AB,CE=
AC,
∴BD=CE,
∵在△DBC和△ECB中,
,
∴△DBC≌△ECB,(SAS)
∴BE=CD.
∴∠ABC=∠ACB=69°,
∵△ADB是等腰直角三角形,
∴∠DBA=45°,
∴∠DBC=∠DBA+∠ABC=114°;
(2)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵△ADB、△ACE是等腰直角三角形,
∴∠DBA=∠ECA=45°,
∴∠DBC=∠ECB,
∵AB=AC,BD=
| 2 |
| 2 |
∴BD=CE,
∵在△DBC和△ECB中,
|
∴△DBC≌△ECB,(SAS)
∴BE=CD.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△DBC≌△ECB是解题的关键.

练习册系列答案
相关题目
方程2-
=3-
,去分母得( )
| 2x-4 |
| 3 |
| x+1 |
| 2 |
| A、12-(4x-8)=18-3(x+1) |
| B、12-3(2x-4)=18-3(x+1) |
| C、12-(2x-4)=18-(x+1) |
| D、6-2(2x-4)=9-(x+1) |
 已知:如图,⊙O的半径OA=16cm,OC⊥AB于C点,sin∠AOC=
已知:如图,⊙O的半径OA=16cm,OC⊥AB于C点,sin∠AOC= 如图所示,在平行四边形ABCD中,已知AD=1,AB=2,对角线BD=2.求对角线AC的长.
如图所示,在平行四边形ABCD中,已知AD=1,AB=2,对角线BD=2.求对角线AC的长.