题目内容
(1)如图1所示,在等边△ABC中,点D是AB边上的动点,以CD为一边,向上作等边△EDC,连接AE,求证:AE∥BC;
(2)如图2所示,将(1)中等边△ABC的形状改成以BC为底边的等腰三角形,所作△EDC相似于△ABC,请问仍有AE∥BC?证明你的结论.

【考点】相似三角形的判定与性质;全等三角形的判定与性质.
【专题】动点型;探究型.
【分析】(1)证明△ACE≌△BCD推出∠ACB=∠EAC即可证.
(2)证明△ABC∽△EDC后可推出∠EAC=∠ACB,由此可证.
【解答】证明:(1)∵△ABC和△EDC是等边三角形
∴∠ACB=∠ECD=60°,AC=CB,EC=DC,
∴∠ACD+∠BCD=∠ACE+∠ACD,
∴∠BCD=∠ACE,
∴△ACE≌△BCD,
∴∠EAC=∠B=60°,
又∵∠ACB=60°,
∴∠ACB=∠EAC,
∴AE∥BC;
(2)仍平行;
∵△ABC∽△EDC,
∴∠ACB=∠ECD,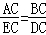 ,
,
∴∠ACD+∠BCD=∠ACE+∠ACD,
∴∠BCD=∠ACE,
∴△AEC∽△BDC,
∴∠EAC=∠B,
又∵∠ACB=∠B,
∴∠EAC=∠ACB,
∴AE∥BC.
【点评】本题考查的是全等三角形的判定以及相似三角形的判定的有关知识.关键是证明△ACE≌△BCD和△ABC∽△EDC.

练习册系列答案
相关题目
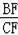
 的值.
的值.


 的解集在数轴上表示为( )
的解集在数轴上表示为( )
 B.
B.
 C.
C.
 D.
D.


 的图象经过点A(2,m),则m的值是( )
的图象经过点A(2,m),则m的值是( )

