题目内容
如图,点E、F分别是▱ABCD的边BC、AD上的点,且CE=AF.
求证:△ABE≌△CDF.


【考点】平行四边形的性质;全等三角形的判定.
【专题】证明题.
【分析】由点E、F分别是▱ABCD的边BC、AD上的点,且CE=AF,可得AB=CD,∠B=∠D,BE=CF,则可由SAS证得:△ABE≌△CDF.
【解答】证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D,
∵CE=AF,
∴AD﹣AF=BC﹣CE,
即BE=DF,
在△ABE和△CDF中,

 ,
,
∴△ABE≌△CDF(SAS).
【点评】此题考查了平行四边形的性质以及全等三角形的判定.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目

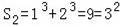
 ;
;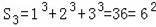
 ;
;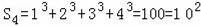
 ;
;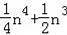
 B.
B.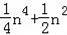
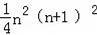
 D.
D.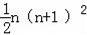




 ,
,



 ,y=2,求代数式
,y=2,求代数式 -2(
-2( )+(
)+( )的值。
)的值。 的值为0,则x的值为__________.
的值为0,则x的值为__________.