题目内容
7.下列计算正确的是( )| A. | $\sqrt{(-5)^{2}}$=-5 | B. | (x3)2=x5 | C. | x6÷x3=x2 | D. | ($\frac{1}{2}$)-2=4 |
分析 分别利用二次根式的性质以及结合幂的乘方运算法则以及同底数幂的乘法运算法则、负指数幂的性质化简求出答案.
解答 解:A、$\sqrt{(-5)^{2}}$=5,故此选项错误;
B、(x3)2=x6,故此选项错误;
C、x6÷x3=x3,故此选项错误;
D、($\frac{1}{2}$)-2=4,正确.
故选:D.
点评 此题主要考查了二次根式的性质以及幂的乘方运算以及同底数幂的乘法运算、负指数幂的性质等知识,正确掌握相关运算法则是解题关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
17.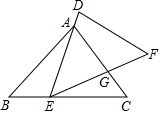 如图,已知△ABC和△DEF,点E在BC边上,点A在DE边上,边EF和边AC相交于点G.如果AE=EC,∠AEG=∠B,那么添加下列一个条件后,仍无法判定△DEF与△ABC一定相似的是( )
如图,已知△ABC和△DEF,点E在BC边上,点A在DE边上,边EF和边AC相交于点G.如果AE=EC,∠AEG=∠B,那么添加下列一个条件后,仍无法判定△DEF与△ABC一定相似的是( )
 如图,已知△ABC和△DEF,点E在BC边上,点A在DE边上,边EF和边AC相交于点G.如果AE=EC,∠AEG=∠B,那么添加下列一个条件后,仍无法判定△DEF与△ABC一定相似的是( )
如图,已知△ABC和△DEF,点E在BC边上,点A在DE边上,边EF和边AC相交于点G.如果AE=EC,∠AEG=∠B,那么添加下列一个条件后,仍无法判定△DEF与△ABC一定相似的是( )| A. | $\frac{AB}{BC}$=$\frac{DE}{EF}$ | B. | $\frac{AD}{AE}$=$\frac{GF}{GE}$ | C. | $\frac{AG}{AC}$=$\frac{EG}{EF}$ | D. | $\frac{ED}{EF}$=$\frac{EG}{EA}$ |
15.关于x的方程(4-a)x${\;}^{{a}^{2}-3a-2}$-ax-5=0是一元二次方程,则它的一次项系数是( )
| A. | -1 | B. | 1 | C. | 4 | D. | 4或-1 |
2.已知m-n=7,mn=8,则(m+n)2的值为( )
| A. | 81 | B. | 64 | C. | 17 | D. | 15 |
19.一个不透明的袋子中装有3个白球和若干个黑球,它们除颜色外完全相同,从袋子中随机摸出一球,记下颜色并放回,重复该实验多次,发现摸到白球的频率稳定在0.6,则可判断袋子中黑球的个数为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
16.在?ABCD中,若∠A=40°,则∠C=( )
| A. | 140° | B. | 130° | C. | 50° | D. | 40° |
11.一直角三角形三边长分别为a,a,c,那么由an,an,cn(n为自然数)为三边组成的三角形一定是( )
| A. | 等腰三角形 | B. | 等腰直角三角形 | C. | 钝角三角形 | D. | 任意三角形 |
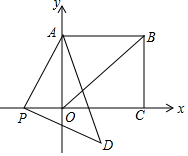 如图,在平面直角坐标系中,四边形ABCO为正方形,A点坐标为(0,2),点P为x轴负半轴上一动点,以AP为直角作等腰直角三角形APD,∠APD=90°(点D落在第四象限)
如图,在平面直角坐标系中,四边形ABCO为正方形,A点坐标为(0,2),点P为x轴负半轴上一动点,以AP为直角作等腰直角三角形APD,∠APD=90°(点D落在第四象限)