题目内容
12.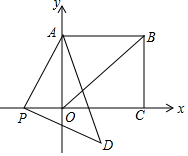 如图,在平面直角坐标系中,四边形ABCO为正方形,A点坐标为(0,2),点P为x轴负半轴上一动点,以AP为直角作等腰直角三角形APD,∠APD=90°(点D落在第四象限)
如图,在平面直角坐标系中,四边形ABCO为正方形,A点坐标为(0,2),点P为x轴负半轴上一动点,以AP为直角作等腰直角三角形APD,∠APD=90°(点D落在第四象限)(1)当点P的坐标为(-1,0)时,求点D的坐标;
(2)点P在移动的过程中,点D是否在直线y=x-2上?请说明理由;
(3)连接OB交AD于点G,求证:AG=DG.
分析 (1)如图1中,作DH⊥OC于H.只要证明△APO≌△PDH,推出PH=OA=2,DH=OP=1即可.
(2)如图2中,作射线CD,设AD交PC于G.由△AGC∽△PGD,推出$\frac{AG}{PG}$=$\frac{CG}{GD}$,推出$\frac{AG}{CG}$=$\frac{PG}{GD}$,由∠AGP=∠CGD,推出△AGP∽△CGD,推出∠PAG=∠GCD=45°,推出∠ACD=90°,即CD⊥AC,求出直线CD的解析式即可解决问题.
(3)如图3中,连接CG、AC、CD.由△GBA≌△GBC,推出GA=GC,只要证明GC=GD即可解决问题.
解答 解:(1)如图1中,作DH⊥OC于H.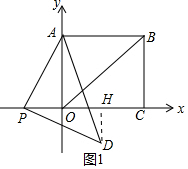
∵四边形AOCB是正方形,A(0,2),P(-1,0),
∴∠AOP=∠PHD=∠APD=90°,OA=2,OP=1,
∵∠APO+∠DPH+90°,∠DPH+∠PDH=90°,
∴∠APO=∠PDH,
在△APO和△PDH中,
$\left\{\begin{array}{l}{∠AOP=∠PHD}\\{∠APO=∠PDH}\\{PA=PD}\end{array}\right.$,
∴△APO≌△PDH,
∴PH=OA=2,DH=OP=1,
∴OH=1,
∴D(1,-1).
(2)如图2中,作射线CD,设AD交PC于G.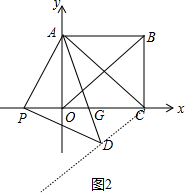
∵∠GCA=∠GDP=45°,∠AGC=∠PGD,
∴△AGC∽△PGD,
∴$\frac{AG}{PG}$=$\frac{CG}{GD}$,
∴$\frac{AG}{CG}$=$\frac{PG}{GD}$,∵∠AGP=∠CGD,
∴△AGP∽△CGD,
∴∠PAG=∠GCD=45°,
∴∠ACD=90°,
∴CD⊥AC,
∵直线AC的解析式为y=-x+2,
∴直线CD的解析式为y=x-2,
∴点D在直线CD上.
(3)如图3中,连接CG、AC、CD.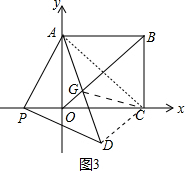
∵四边形OABC是正方形,
∴BA=BC,∠GBA=∠GBC,∵BG=BG,
∴△GBA≌△GBC,
∴GA=GC,
∴∠GAC=∠GCA,
∵∠ACD=90°,
∴∠GDC+∠GAC=90°,∠GCB+∠GCA=90°,
∴∠GDC=∠GCD,
∴GC=GD,
∴AG=GD.
点评 本题考查一次函数综合题、等腰直角三角形的性质、全等三角形的判定和性质、相似三角形的判定角性质等知识,解题的关键是正确寻找全等三角形解决问题,学会添加常用辅助线,构造相似三角形解决问题,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案| A. | 4,32 | B. | 4,-32 | C. | -4,32 | D. | -4,-32 |
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
| A. | $\frac{a}{-a-b}$ | B. | -$\frac{a}{a+b}$ | C. | $\frac{a}{a+b}$ | D. | -$\frac{a}{a-b}$ |
| A. | $\sqrt{(-5)^{2}}$=-5 | B. | (x3)2=x5 | C. | x6÷x3=x2 | D. | ($\frac{1}{2}$)-2=4 |
| A. | 随机事件发生的概率等于0.5 | |
| B. | 5名同学期末数学成绩是92,95,95,98,110,则他们众数是95 | |
| C. | 射击运动员甲、乙分别射击10次且击中环数的方差分别是0.5和1.2,则乙较稳定 | |
| D. | 要了解一批日光灯的质量,可采用全面调查的办法 |
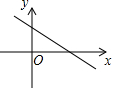 若一次函数y=kx+b的图象如图所示,则k,b的值可能为( )
若一次函数y=kx+b的图象如图所示,则k,b的值可能为( )| A. | k=3,b=3 | B. | k=3,b=-3 | C. | k=-3,b=3 | D. | k=-3,b=-3 |