题目内容
9. 如图,AD∥BE,AC,BC分别平分∠DAB和∠EBA,试判断AC和BC的位置关系,并说明理由.
如图,AD∥BE,AC,BC分别平分∠DAB和∠EBA,试判断AC和BC的位置关系,并说明理由.
分析 根据平行线的性质得到∠DAB+∠ABE=180°,根据角平分线的定义得到∠CAB=$\frac{1}{2}∠$DAB,∠ABC=$\frac{1}{2}∠$ABE,于是得到结论.
解答 解:AC⊥BC,
理由:∵AD∥BE,
∴∠DAB+∠ABE=180°,
∵AC,BC分别平分∠DAB和∠EBA,
∴∠CAB=$\frac{1}{2}∠$DAB,∠ABC=$\frac{1}{2}∠$ABE,
∴∠CAB+∠ABC=90°,
∴∠C=90°,
∴AC⊥BC.
点评 本题考查了平行线的性质,角平分线的定义,三角形的内角和,熟练掌握平行线的定义是解题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
17.下表是某种图书的册数与价格之间的关系,请根据表中数据解答下列问题:
(1)完成下表:
(2)根据表格可知价格(y)与册数(x)的函数解析式为y=7.5x,自变量的取值范围为x>0,且x为整数.
(3)画出函数图象.
(4)当售出6册时价格是多少元?
(1)完成下表:
| 册数(x) | 1 | 2 | 3 | … | |
| 价格(y) | 7.5 | 15 | 30 | … |
(3)画出函数图象.
(4)当售出6册时价格是多少元?
18.为了解某校八、九年级学生的睡眠情况,随机抽取了该校八、九年级部分学生进行调查,已知抽取的八年级与九年级的学生人数相同,利用抽样所得的数据绘制如下统计图和统计表.
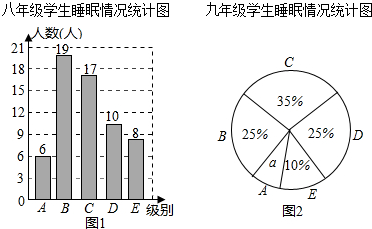
睡眠情况分组表(单位:时)
根据图表提供的信息,回答下列问题:
(1)求统计图中的a;
(2)抽取的样本中,九年级学生睡眠时间在C组的有多少人?
(3)睡眠时间少于6.5小时为严重睡眠不足,则从该校八、九年级各随机抽一名学生,被抽到的这两位学生睡眠严重不足的可能性分别有多大?

睡眠情况分组表(单位:时)
| 组别 | 睡眠时间x |
| A | 4.5≤x<5.5 |
| B | 5.5≤x<6.5 |
| C | 6.5≤x<7.5 |
| D | 7.5≤x<8.5 |
| E | 8.5≤x<9.5 |
(1)求统计图中的a;
(2)抽取的样本中,九年级学生睡眠时间在C组的有多少人?
(3)睡眠时间少于6.5小时为严重睡眠不足,则从该校八、九年级各随机抽一名学生,被抽到的这两位学生睡眠严重不足的可能性分别有多大?
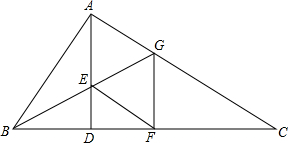 如图,AD是Rt△ABC斜边BC上的高,∠ABC的角平分线交AD于E,交AC于G.
如图,AD是Rt△ABC斜边BC上的高,∠ABC的角平分线交AD于E,交AC于G.