题目内容
12.计算:(1)$\sqrt{27}$-$\sqrt{12}$+$\sqrt{45}$
(2)$\frac{3-\sqrt{18}}{\sqrt{3}}$+$\sqrt{\frac{3}{2}}$.
分析 (1)先把二次根式化为最简二次根式,然后合并即可;
(2)先进行分母有理化,然后化简后合并即可.
解答 解:(1)原式=3$\sqrt{3}$-2$\sqrt{3}$+3$\sqrt{5}$
=$\sqrt{3}$+3$\sqrt{5}$;
(2)原式=$\frac{3\sqrt{3}-\sqrt{18×3}}{\sqrt{3}×\sqrt{3}}$+$\frac{\sqrt{6}}{2}$
=$\sqrt{3}$-$\sqrt{6}$+$\frac{\sqrt{6}}{2}$
=$\sqrt{3}$-$\frac{\sqrt{6}}{2}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
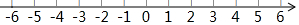 邮递员骑摩托车从邮局出发,先向西骑行2km到达A村,继续向西骑行3km到达B村,然后向东骑行9km到C村,最后回到邮局.
邮递员骑摩托车从邮局出发,先向西骑行2km到达A村,继续向西骑行3km到达B村,然后向东骑行9km到C村,最后回到邮局.