题目内容
20.已知a、b互为相反数且a≠0,c、d互为倒数,m的绝对值是最小的正整数,求|m|-$\frac{a}{b}$+$\frac{2007(a+b)}{2008}$-cd的值.分析 根据互为相反数的两个数的和等于0可得a+b=0,互为倒数的两个数的乘积是1可得cd=1,根据绝对值的性质求出m的值,然后代入代数式进行计算即可得解.
解答 解:∵a、b互为相反数且a≠0,
∴a+b=0,
∴$\frac{a}{b}$=-1,
又∵c、d互为倒数,
∴cd=1,
∵m的绝对值是最小的正整数,
∴m=±1,
∴|m|-$\frac{a}{b}$+$\frac{2007(a+b)}{2008}$-cd=1-(-1)+0-1=1+1-1=1.
点评 本题考查了代数式求值,主要利用了相反数的定义,倒数的定义,绝对值的性质,熟记概念与性质是解题的关键.

练习册系列答案
相关题目
15.两个有理数的和与积都是负数,那么这两个有理数( )
| A. | 都是负数 | B. | 一正一负,其中正数的绝对值较大 | ||
| C. | 都是正数 | D. | 一正一负,其中负数的绝对值较大 |
 已知AB=DC,BE=CF,只要补充∠B=∠C,或AB∥CD,就可以证明△ABE≌△DCF.
已知AB=DC,BE=CF,只要补充∠B=∠C,或AB∥CD,就可以证明△ABE≌△DCF.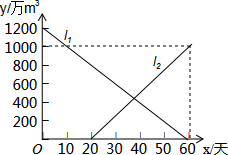 今年夏天,重庆各区持续高温日数达到历史之最,受持续高温和连日无雨的影响,重庆某水库的蓄水量随时间的增加而减少,已知原有蓄水量y1(万m3)与干旱持续时间x(天)的关系如图中线段l1所示,针对这种干旱情况,从第20天开始向水库注水,注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其他因素).若总蓄水量不多于900万m3为严重干旱,则该水库发生严重干旱时的天数为15≤x≤40天.
今年夏天,重庆各区持续高温日数达到历史之最,受持续高温和连日无雨的影响,重庆某水库的蓄水量随时间的增加而减少,已知原有蓄水量y1(万m3)与干旱持续时间x(天)的关系如图中线段l1所示,针对这种干旱情况,从第20天开始向水库注水,注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其他因素).若总蓄水量不多于900万m3为严重干旱,则该水库发生严重干旱时的天数为15≤x≤40天.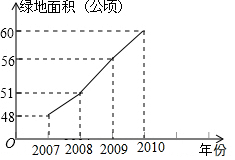 美化城市,改善人们的居住环境已成为城市建设的一项重要内容.某市城区近几年来,通过拆迁旧房、植树、种草、修建公园等措施,使城区绿地面积不断增加(如图所示).
美化城市,改善人们的居住环境已成为城市建设的一项重要内容.某市城区近几年来,通过拆迁旧房、植树、种草、修建公园等措施,使城区绿地面积不断增加(如图所示).