题目内容
 CD是⊙O的直径,AB是弦,且AB⊥CD,垂足是E,如果CE=2、AB=8,那么ED=
CD是⊙O的直径,AB是弦,且AB⊥CD,垂足是E,如果CE=2、AB=8,那么ED=考点:垂径定理,勾股定理
专题:计算题
分析:连结OA,如图,根据垂径定理得AE=BE=
AB=4,在Rt△OAE中利用勾股定理得OE2+AE2=OA2,即(r-2)2+42=r2,解方程得到r=5,然后利用直径CD减去CE即可得到DE.
| 1 |
| 2 |
解答:解:连结OA,如图,
∵AB⊥CD,
∴AE=BE=
AB=4,
在Rt△OAE中,OA=r,OE=OC-CE=r-2,AE=4,
∵OE2+AE2=OA2,
∴(r-2)2+42=r2,解得r=5,
∴DE=CD-CE=10-2=8.
故答案为8,5.

∵AB⊥CD,
∴AE=BE=
| 1 |
| 2 |
在Rt△OAE中,OA=r,OE=OC-CE=r-2,AE=4,
∵OE2+AE2=OA2,
∴(r-2)2+42=r2,解得r=5,
∴DE=CD-CE=10-2=8.
故答案为8,5.
点评:本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一个水利勘察队沿河向上游走了5
千米,又继续向上游走了5
千米,然后向下游走了4
千米,接着又向下游走了5
千米,这时勘察队在出发点的( )
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
A、上游1
| ||
| B、下游1千米处 | ||
C、上游
| ||
D、下游
|
下列说法不正确的是( )
| A、经过平移,图形的形状和大小都不改变 |
| B、经过旋转,图形的形状和大小发生了改变 |
| C、轴对称图形,对称轴两旁的部分一定完全重合 |
| D、平移中,图形上每个点沿直线运动 |
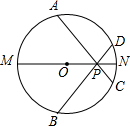 如图,P为⊙O的直径MN上一点,过P作弦AC、BD使∠APM=∠BPM,求证:PA=PB.
如图,P为⊙O的直径MN上一点,过P作弦AC、BD使∠APM=∠BPM,求证:PA=PB. 作图题:作线段AB的垂直平分线(尺规作图,不写作法,保留作图痕迹)
作图题:作线段AB的垂直平分线(尺规作图,不写作法,保留作图痕迹) 如图:△ABC中,点O是AC边上一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
如图:△ABC中,点O是AC边上一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F. 如图,已知△ABE≌△ACD,求证:∠1=∠2.
如图,已知△ABE≌△ACD,求证:∠1=∠2.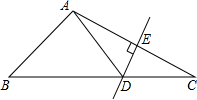 如图,在△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为15cm,求△ABC的周长.
如图,在△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为15cm,求△ABC的周长.