题目内容
11.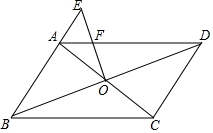 如图,在?ABCD中,对角线AC、BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F.若CD=5,BC=8,AE=2,则AF=$\frac{16}{9}$.
如图,在?ABCD中,对角线AC、BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F.若CD=5,BC=8,AE=2,则AF=$\frac{16}{9}$.
分析 过O点作OM∥AD,求出AM和MO的长,利用△AEF∽△MEO,得到关于AF的比例式,求出AF的长即可.
解答 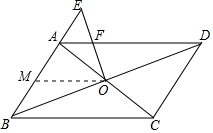 解:过O点作OM∥AD,
解:过O点作OM∥AD,
∵四边形ABCD是平行四边形,
∴OB=OD,
∴OM是△ABD的中位线,
∴AM=BM=$\frac{1}{2}$AB=$\frac{5}{2}$,OM=$\frac{1}{2}$BC=4,
∵AF∥OM,
∴△AEF∽△MEO,
∴$\frac{AE}{EM}$=$\frac{AF}{OM}$,
∴$\frac{2}{2+\frac{5}{2}}$=$\frac{AF}{4}$,
∴AF=$\frac{16}{9}$,
故答案为$\frac{16}{9}$.
点评 本题考查矩形的性质、三角形的中位线定理、平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,学会用方程的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
2.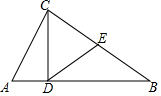 如图,△ABC中,E为BC边的中点,CD⊥AB,AB=2,AC=1,DE=$\frac{\sqrt{3}}{2}$,则∠CDE+∠ACD=( )
如图,△ABC中,E为BC边的中点,CD⊥AB,AB=2,AC=1,DE=$\frac{\sqrt{3}}{2}$,则∠CDE+∠ACD=( )
 如图,△ABC中,E为BC边的中点,CD⊥AB,AB=2,AC=1,DE=$\frac{\sqrt{3}}{2}$,则∠CDE+∠ACD=( )
如图,△ABC中,E为BC边的中点,CD⊥AB,AB=2,AC=1,DE=$\frac{\sqrt{3}}{2}$,则∠CDE+∠ACD=( )| A. | 60° | B. | 75° | C. | 90° | D. | 105° |
6.为确保广大居民家庭基本用水需求的同时鼓励家庭节约用水,对居民家庭每户每月用水量采用分档递增收费的方式,每户每月用水量不超过基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费.为对基本用水量进行决策,随机抽查2000户居民家庭每户每月用水量的数据,整理绘制出下面的统计表:
(1)为确保70%的居民家庭每户每月的基本用水量需求,那么每户每月的基本用水量最低应确定为多少立方米?
(2)若将(1)中确定的基本用水量及其以内的部分按每立方米1.8元交费,超过基本用水量的部分按每立方米2.5元交费.设x表示每户每月用水量(单位:m3),y表示每户每月应交水费(单位:元),求y与x的函数关系式;
(3)某户家庭每月交水费是80.9元,请按以上收费方式计算该家庭当月用水量是多少立方米?
| 用户每月用水量(m3) | 32及其以下 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43及其以上 |
| 户数(户) | 200 | 160 | 180 | 220 | 240 | 210 | 190 | 100 | 170 | 120 | 100 | 110 |
(2)若将(1)中确定的基本用水量及其以内的部分按每立方米1.8元交费,超过基本用水量的部分按每立方米2.5元交费.设x表示每户每月用水量(单位:m3),y表示每户每月应交水费(单位:元),求y与x的函数关系式;
(3)某户家庭每月交水费是80.9元,请按以上收费方式计算该家庭当月用水量是多少立方米?
3.已知某种细菌的直径为0.0000302mm,用科学记数法表示为( )
| A. | 3.02×10-5mm | B. | 30.2×10-6mm | C. | 302×10-4mm | D. | 302×10-8mm |
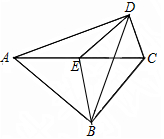 如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,ED,BD.若∠BAD=58°,则∠EBD的度数为32度.
如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,ED,BD.若∠BAD=58°,则∠EBD的度数为32度.