题目内容
1.427+41000+4n为完全平方数,求n的值.1972或513或-947.分析 通过提公因式,把原式整理成完全平方式的形式,从而推出n的值.
解答 解:因为427+41000+4n=254(1+2•21945+22n-54),
所以当2n-54=2×1945,即n=1972时,上式为完全平方数,
因为427+41000+4n=254(1+21946+2•22n-53),
所以当1946=2×(2n-53),即n=513时,上式为完全平方数,
因为427+41000+4n=254(21946+2•2-1+22n-54),
2973•2n-27=2-1,即n=-947时,上式为完全平方数,
故答案为1972或513或-947.
点评 此题主要考查了完全平方数,正确利用完全平方数的性质是解题关键.

练习册系列答案
相关题目
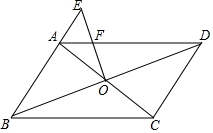 如图,在?ABCD中,对角线AC、BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F.若CD=5,BC=8,AE=2,则AF=$\frac{16}{9}$.
如图,在?ABCD中,对角线AC、BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F.若CD=5,BC=8,AE=2,则AF=$\frac{16}{9}$.