题目内容
4.△ABC中,AB=4,AC=2,在AC的延长线上取一点D,当CD=6时,△ADB∽△ABC.分析 由于两三角形有公共角,则根据两组对应边的比相等且夹角对应相等的两个三角形相似,当$\frac{AD}{AB}$=$\frac{AB}{AC}$时,△ADB∽△ABC,然后利用相似比可计算出AD,从而可得CD的长.
解答 解:如图,
∵∠BAC=∠DAB,
∴当$\frac{AD}{AB}$=$\frac{AB}{AC}$时,△ADB∽△ABC,
即$\frac{AD}{4}$=$\frac{4}{2}$,解得AD=8,
∴CD=AD-AC=8-2=6.
故答案为6.
点评 本题考查了相似三角形的性质:两组对应边的比相等且夹角对应相等的两个三角形相似.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
19.甲种食品保鲜适宜温度是1℃~5℃,乙种食品保鲜适宜温度是3℃~8℃,将两种食品放在一起保鲜,则适宜的温度是( )
| A. | 1℃~8℃ | B. | 3℃~5℃ | C. | 5℃~8℃ | D. | 1℃~3℃ |
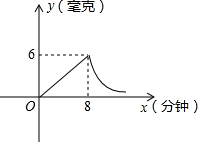 为了预防流感,市教育局要求学校利用星期天用药熏消毒法对所有教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比;药物释放完毕后,y(毫克)与时间x(分钟)成反比,如图所示.现测得8分钟后药物释放完毕,此时室内每立方米空气中的含药量为6毫克,据图中提供的信息,解答下列问题:
为了预防流感,市教育局要求学校利用星期天用药熏消毒法对所有教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比;药物释放完毕后,y(毫克)与时间x(分钟)成反比,如图所示.现测得8分钟后药物释放完毕,此时室内每立方米空气中的含药量为6毫克,据图中提供的信息,解答下列问题: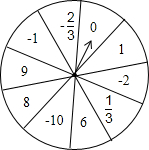 如图是小芳设计可自由的均匀转盘,将其等分为10个扇形,每个扇形有1个有理数,想想看,转得下列各数的概率是多少?
如图是小芳设计可自由的均匀转盘,将其等分为10个扇形,每个扇形有1个有理数,想想看,转得下列各数的概率是多少?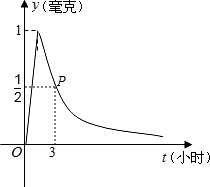 为了预防流感,某图书馆用药熏消毒法对其阅览厅进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t成反比例(如图所示).根据图中提供的信息,解答下列问题:
为了预防流感,某图书馆用药熏消毒法对其阅览厅进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t成反比例(如图所示).根据图中提供的信息,解答下列问题: