题目内容
16.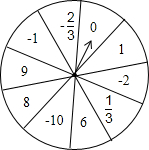 如图是小芳设计可自由的均匀转盘,将其等分为10个扇形,每个扇形有1个有理数,想想看,转得下列各数的概率是多少?
如图是小芳设计可自由的均匀转盘,将其等分为10个扇形,每个扇形有1个有理数,想想看,转得下列各数的概率是多少?(1)转得正整数;
(2)转得正数;
(3)转得绝对值<6的数;
(4)转得绝对值≥6的数;
(5)若小芳和小锐做游戏,转得正整数小芳获胜,转得绝对值≥6的数小锐获胜,这个游戏公平吗?
分析 根据题意找出符合条件的数,再利用概率公式分别计算其概率即可.
解答 解:(1)10个数中正整数有1,6,8,9,共四个,故转得正整数的概率=$\frac{4}{10}$=$\frac{2}{5}$;
(2)10个数中正数有1,$\frac{1}{3}$,6,8,9,共5个,故转得正数的概率=$\frac{5}{10}$=$\frac{1}{2}$;
(3)10个数中绝对值小于6的数有0,1,-2,-$\frac{2}{3}$,-1,-共6个,故转得绝对值小于6的数的概率=$\frac{6}{10}$=$\frac{3}{5}$;
(4)10个数中绝对值大于等于6的数有-10,8,9,6共4个,故转得绝对值大于等于6的数的概率=$\frac{4}{10}$=$\frac{2}{5}$;
(5)由(1)可知转得正整数的概率=$\frac{2}{5}$,转得绝对值≥6的概率=$\frac{2}{5}$,
所以这个游戏公平.
点评 本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个人取胜的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
11.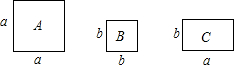 有足够多的如图所示的正方形和长方形卡片,如果要拼成一个长为(2a+b),宽为(a+b)的长方形,则需要A、B、C类卡片的张数分别为( )
有足够多的如图所示的正方形和长方形卡片,如果要拼成一个长为(2a+b),宽为(a+b)的长方形,则需要A、B、C类卡片的张数分别为( )
 有足够多的如图所示的正方形和长方形卡片,如果要拼成一个长为(2a+b),宽为(a+b)的长方形,则需要A、B、C类卡片的张数分别为( )
有足够多的如图所示的正方形和长方形卡片,如果要拼成一个长为(2a+b),宽为(a+b)的长方形,则需要A、B、C类卡片的张数分别为( )| A. | 1、2、3 | B. | 2、1、3 | C. | 1、3、2 | D. | 2、3、1 |
1.下列式子成立的是( )
| A. | $\frac{b}{a}$+$\frac{2}{b}$=$\frac{b+2}{a+b}$ | B. | ($\frac{-y}{2x}$)2=$\frac{{y}^{2}}{2x}$ | C. | y2÷y-3=y-1 | D. | $\frac{a}{a-b}$-$\frac{b}{a-b}$=1 |
6.已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表:
(1)求该二次函数的关系式;
(2)当x为何值时,y有最小值,最小值是多少?
(3)若A(m,y1),B(m+1,y2)两点都在该函数的图象上,其中m<1,试比较y1与y2的大小.
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 10 | 5 | 2 | 1 | 2 | 5 | … |
(2)当x为何值时,y有最小值,最小值是多少?
(3)若A(m,y1),B(m+1,y2)两点都在该函数的图象上,其中m<1,试比较y1与y2的大小.