Question

20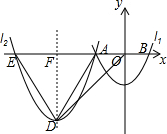．如图，在平面直角坐标系中，抛物线l₁与x轴交于点A，B，与y轴交于点C，l₁的解析式为y=$\frac{1}{2}$x²-2，若将抛物线l₁平移，使平移后的抛物线l₂经过点A，对称轴为直线x=-6，抛物线l₂与x轴的另一个交点是E，顶点是D，连结OD，AD，ED．
（1）求抛物线l₂的解析式；
（2）求证：△ADE∽△DOE；
（3）半径为1的⊙P的圆心P沿着直线x=-6从点D运动到F（-6，0），运动速度为1单位/秒，运动时间为t秒，⊙P绕着点C顺时针旋转90°得⊙P₁，随着⊙P的运动，求P₁的运动路径长以及当⊙P₁与y轴相切的时候t的值．

Answer 1

分析 （1）设抛物线l₂的解析式为y=$\frac{1}{2}$（x+a）²+c，由抛物线l₁的解析式，可求出点A的坐标，由抛物线l₂的对称轴以及点A的坐标即可求出a、c的值，由此得出结论；
（2）由抛物线的对称性可知△DAE为等腰三角形，由l₂的解析式可得出D点、E点坐标，根据两点间的距离公式可求出OE=OD，由两等腰三角形一个底角相等即可得出△ADE∽△DOE；
（3）由旋转的特性可知P₁的运动路径长与P的运动路径长相等，由圆与直线相切可得出相切时D′P₁的长度，由时间=路程÷速度即可得出结论．

解答 解：（1）设抛物线l₂的解析式为y=$\frac{1}{2}$（x+a）²+c，
∵抛物线l₂的对称轴为x=-6，
∴a=6．
令l₁的解析式y=$\frac{1}{2}$x²-2=0，
解得：x=±2．
∴A点的坐标为（-2，0），B点的坐标为（2，0）．
将点A（-2，0）代入l₂的解析式中，得$\frac{1}{2}$×（-2+6）²+c=0，
解得：c=-8．
故抛物线l₂的解析式为y=$\frac{1}{2}（x+6）^{2}$-8．
（2）证明：令l₂的解析式y=$\frac{1}{2}（x+6）^{2}$-8=0，
解得x=-10，或x=-2，
故点E的坐标为（-10，0）．
由抛物线的对称性可知△ADE为等腰三角形．
∵点O（0，0），点E（-10，0），点D（-6，-8），
∴OE=0-（-10）=10，OD=$\sqrt{（-6）^{2}+（-8）^{2}}$=10，
∴OE=OD，
即△OED为等腰三角形，
又∵∠DEA=∠OED，且两者均为底角，
∴△ADE∽△DOE．
（3）过点C作CN⊥DF于点N，根据题意画出图形如图所示．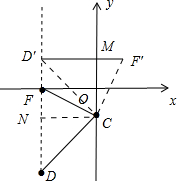

点D旋转后到达D′处，点F旋转后到达F′处．
根据旋转的性质可知D′F′=DF，
∵点D（-6，-8），点F（-6，0），
∴P₁的运动路径长为DF=8．
∵DF∥y轴，
∴D′F′∥x轴，
∴四边形NCMD′为平行四边，
∴D′M=NC．
∵l₁的解析式为y=$\frac{1}{2}$x²-2，
∴点C的坐标为（0，-2），
∴点N的坐标为（-6，-2），
∴NC=0-（-6）=6．
∵⊙P₁的半径为1，
∴当D′P₁=D′M±1时，⊙P₁与y轴相切，
此时D′P₁=5，或D′P₁=7．
∵⊙P的运动速度为1单位/秒，
∴⊙P₁的运动速度为1单位/秒，
∴运算时间为5秒或7秒．

点评 本题考查了待定系数法求函数解析式、两点间的距离公式、相似三角形的判定以及旋转的性质，解题的关键：（1）利用待定系数法求函数解析式；（2）找出△OED为等腰三角形；（3）根据旋转的性质作出图形，数形结合解决问题．本题属于中档题，（1）（2）难度不大；（3）涉及到旋转，对于初中生来说旋转的题都有很大的难度，但该题巧合在DF于y轴平行，降低了该问的难度，作该问时，可以过点C作CN⊥DF于N，经旋转CN重合与y轴，可结合⊙P相切于直线y=-2来解决时间的问题．