题目内容
1.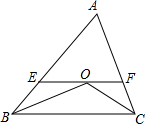 在△ABC中,AB≠AC,∠ABC和∠ACB的平分线交于点O,过O作EF∥BC交AB于E,交AC于F.请你写出图中所有等腰三角形,并探究EF、BE、FC之间的关系.
在△ABC中,AB≠AC,∠ABC和∠ACB的平分线交于点O,过O作EF∥BC交AB于E,交AC于F.请你写出图中所有等腰三角形,并探究EF、BE、FC之间的关系.
分析 根据等腰三角形的判定,可得等腰三角形,根据角平分线的性质,可得∠EBO与CBO,∠FOC与∠FCO的关系,根据平行线的性质,可得∠EOB与∠CBO,∠FOC与∠BCO的关系,根据等腰三角形的判定,可得BE与EO,CF与FO的关系,根据线段的和差,可得答案.
解答 解:等腰三角形有:等腰△ABC,等腰△BEO,等腰△CFO,等腰△BOC,等腰△AEF,BE+CF=EF,
理由如下:
∵BO平分∠ABC,CO平分∠ACB,
∴∠EBO=CBO,∠FOC=∠FCO.
∵EF∥BC,
∴∠EOB=∠CBO,∠FOC=∠BCO,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=EO,CF=FO.
∵EO+OF=EF,
∴BE+CF=EF.
点评 本题考查了等腰三角形的判定与性质,利用了等腰三角形的判定与性质,角平分线的性质,平行线的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.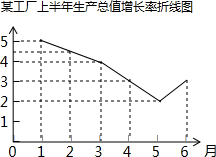 某工厂上半年生产总值增长率的变化情况如图所示,从图看,下列结论中不正确的是( )
某工厂上半年生产总值增长率的变化情况如图所示,从图看,下列结论中不正确的是( )
 某工厂上半年生产总值增长率的变化情况如图所示,从图看,下列结论中不正确的是( )
某工厂上半年生产总值增长率的变化情况如图所示,从图看,下列结论中不正确的是( )| A. | 1~5月份生产总值增长率逐月减少 | |
| B. | 6月份生产总值的年增长率开始回升 | |
| C. | 这半年中每月的生产总值不断增长 | |
| D. | 这半年中每月的生产总值有增有减 |
10.分式方程$\frac{2}{x-2}+\frac{3x}{2-x}=-1$的解为( )
| A. | 1 | B. | 2 | C. | 无解 | D. | 0 |
 如图,等边△ABC中,AD是中线,AD=AE,则∠EDC=15°.
如图,等边△ABC中,AD是中线,AD=AE,则∠EDC=15°.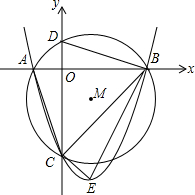 如图,已知抛物线y=ax2+bx-3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为$\sqrt{5}$,设⊙M与y轴交于D,抛物线的顶点为E.
如图,已知抛物线y=ax2+bx-3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为$\sqrt{5}$,设⊙M与y轴交于D,抛物线的顶点为E.