题目内容
4.已知四边形ABCD各顶点的坐标分别是A(0,0)、B(1,2)、C(5,4)、D(7,0).(1)建立平面直角坐标系,并画出四边形ABCD;
(2)求四边形ABCD的面积.
分析 (1)建立平面直角坐标系,然后确定出点A、B、C、D的位置,再顺次连接即可;
(2)根据点A、B、C、D的位置,用平行于坐标轴的辅助线用“割、补”法去求四边形ABCD的面积.
解答 解:(1)如图所示,四边形ABCD即为所求;
(2)如图所示,过B作BE⊥AD于E,作CF⊥AD于F,
则四边形ABCD的面积=$\frac{1}{2}$×1×2+$\frac{1}{2}$×(2+4)×4+$\frac{1}{2}$×2×4=17.
点评 本题主要考查了坐标与图形性质,解决问题的关键是过已知点向坐标轴作垂线,然后求出相关的线段长,是解决这类问题的基本方法和规律.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
13.下列式子中是分式的是( )
| A. | $\frac{10x}{7}$ | B. | $\frac{9+x}{5}$ | C. | $\frac{100}{20+x}$ | D. | $\frac{2}{5}$ |
1.在数学活动课上,老师出示两张等腰三角形纸片,如图所示.图1的三角形边长分别为4,4,2;图2的三角形的腰长也为4,底角等于图1中三角形的顶角;某学习小组将这两张纸片在同一平面内拼成如图3的四边形OABC,连结AC.该学习小组经探究得到以下四个结论,其中错误的是( )
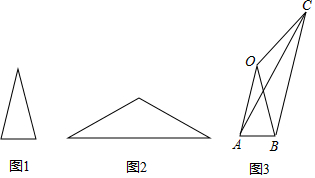

| A. | ∠OCB=2∠ACB | B. | ∠OAB+∠OAC=90° | C. | AC=2$\sqrt{15}$ | D. | BC=4$\sqrt{3}$ |
 如图,在平面直角坐标系中,直线l:y=x-1与x轴交于点A,如图所示依次作正方形A1B1C1O,正方形A2B2C2C1,…,正方形AnBnCnCn-1,使得点A1、A2、A3…An在直线l上,点C1、C2、C3…Cn在y轴正半轴上,请解决下列问题:
如图,在平面直角坐标系中,直线l:y=x-1与x轴交于点A,如图所示依次作正方形A1B1C1O,正方形A2B2C2C1,…,正方形AnBnCnCn-1,使得点A1、A2、A3…An在直线l上,点C1、C2、C3…Cn在y轴正半轴上,请解决下列问题: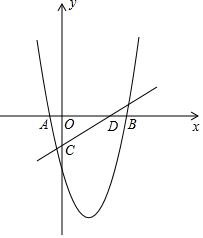 如图,抛物线y=x2+bx+c与x轴交于点A(-1,0),B(5,0)两点,直线y=$\frac{3}{4}$x-3与y轴交于点C,与x轴交于点D,点P时第四象限内的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.
如图,抛物线y=x2+bx+c与x轴交于点A(-1,0),B(5,0)两点,直线y=$\frac{3}{4}$x-3与y轴交于点C,与x轴交于点D,点P时第四象限内的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.
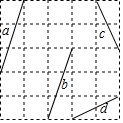 如图,在5×5的正方形网格中,每个小正方形的顶点叫做格点,线段a、b、c、d的端点都在格点上,通过平移其中的两条线段,使得与第三条线段首尾相接组成三角形
如图,在5×5的正方形网格中,每个小正方形的顶点叫做格点,线段a、b、c、d的端点都在格点上,通过平移其中的两条线段,使得与第三条线段首尾相接组成三角形