题目内容
13. 如图,△ABC的三个顶点的坐标分别为A(0,2),B(4,0),C(6,4),求△ABC的周长与面积.
如图,△ABC的三个顶点的坐标分别为A(0,2),B(4,0),C(6,4),求△ABC的周长与面积.
分析 先利用两点间的距离计算出AB、BC、AC的长,则可计算出△ABC的面积,再利用勾股定理的逆定理得到△ABC为直角三角形,∠ABC=90°,然后根据三角形面积公式计算△ABC的面积.
解答 解:∵A(0,2),B(4,0),C(6,4),
∴AB=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,BC=$\sqrt{(6-4)^{2}+(4-0)^{2}}$=2$\sqrt{5}$,AC=$\sqrt{(6-0)^{2}+(4-2)^{2}}$=2$\sqrt{10}$,
∴△ABC的周长=AB+BC+AC=2$\sqrt{5}$+2$\sqrt{5}$+2$\sqrt{10}$=4$\sqrt{5}$+2$\sqrt{10}$;
∵AB2+BC2=AC2,
∴△ABC为直角三角形,∠ABC=90°,
∴△ABC的面积=$\frac{1}{2}$•2$\sqrt{5}$•2$\sqrt{5}$=10.
点评 本题考查了两点间的距离公式:设有两点A(x1,y1),B(x2,y2),则这两点间的距离为AB=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
5.下列运算中正确的是( )
| A. | (ab2)3=ab6 | B. | (3xy)3=9x3y3 | C. | (-2a2)2=4a4 | D. | (ab)3=ab3 |
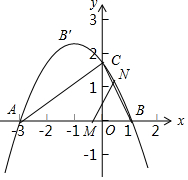 如图,已知点A(-3,0),二次函数y=ax2+bx+$\sqrt{3}$的对称轴为直线x=-1,其图象过点A与x轴交于另一点B,与y轴交于点C.
如图,已知点A(-3,0),二次函数y=ax2+bx+$\sqrt{3}$的对称轴为直线x=-1,其图象过点A与x轴交于另一点B,与y轴交于点C.
 某个立体图形的侧面展开图形如图所示,它的底面是正三角形,这个立体图形一定是三棱柱.
某个立体图形的侧面展开图形如图所示,它的底面是正三角形,这个立体图形一定是三棱柱.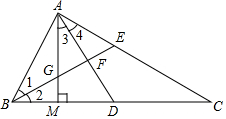 如图,在△ABC中,∠BAC=90°,BE平分∠ABC,AM⊥BC于点M,AD平分∠MAC,交BC于点D,AM交BE于点G.
如图,在△ABC中,∠BAC=90°,BE平分∠ABC,AM⊥BC于点M,AD平分∠MAC,交BC于点D,AM交BE于点G.