题目内容
10.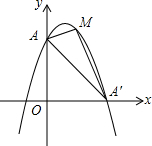 已知,抛物线y=-x2+2x+3与y轴交于A点与x轴正半轴交于A′,点M为第一象限内抛物线上的一动点,问:点M在何处时,△AMA′的面积最大,最大面积为多少.
已知,抛物线y=-x2+2x+3与y轴交于A点与x轴正半轴交于A′,点M为第一象限内抛物线上的一动点,问:点M在何处时,△AMA′的面积最大,最大面积为多少.
分析 连接OM,由二次函数的解析式求出A′坐标,根据三角形面积求出△AMA′的面积,配方即可得到△AMA'的最大面积和M的坐标.
解答 解:连接OM,如图所示: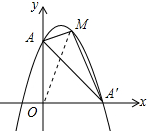
由y=0得:-x2+2x+3=0,
解得:x=-1,或x=3,
∴A′(3,0),
设M点的坐标为:(m,n),
∵点M在抛物线上,
∴n=-m2+2m+3,
∴S△AMA′=S△AMO+S△OMA′-S△AOA′
=$\frac{1}{2}$OA•m+$\frac{1}{2}$OA′•n-$\frac{1}{2}$OA•OA′
=$\frac{3}{2}$(m+n)-$\frac{9}{2}$=$\frac{3}{2}$(m+n-3),
将n=-m2+2m+3代入,原式=-$\frac{3}{2}$(m2-3m)=-$\frac{3}{2}$(m-$\frac{3}{2}$)2+$\frac{27}{8}$,
∵0<m<3,
∵m=$\frac{3}{2}$时,n=$\frac{15}{4}$,△AMA'的面积最大S△AMA'=$\frac{27}{8}$,
∴M($\frac{3}{2}$,$\frac{15}{4}$),
即M的坐标为($\frac{3}{2}$,$\frac{15}{4}$)时,△AMA′的面积最大,最大面积为$\frac{27}{8}$.
点评 本题着重考查了二次函数的最值问题、三角形面积的计算;综合性强,求出三角形的面积是关于m的二次函数是解决问题的关键.

练习册系列答案
相关题目
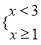 的解集在数轴上表示为
的解集在数轴上表示为 ( )
( ) B.
B. 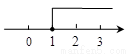 C.
C. 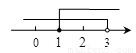 D.
D. 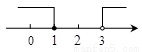
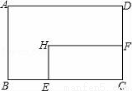
 B.
B.  C.
C.  D.
D. 
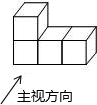 如图,下面这个几何体是由四个相同的边长为2cm正方体组成,画出这个几何体的三视图并求这个几何体的表面积.
如图,下面这个几何体是由四个相同的边长为2cm正方体组成,画出这个几何体的三视图并求这个几何体的表面积.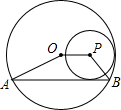 如图,⊙P内切于⊙O,⊙O的弦AB与⊙P相切,且AB∥OP,若⊙O的半径为3,⊙P的半径为1,则四边形ABPO的面积为2$+2\sqrt{2}$.
如图,⊙P内切于⊙O,⊙O的弦AB与⊙P相切,且AB∥OP,若⊙O的半径为3,⊙P的半径为1,则四边形ABPO的面积为2$+2\sqrt{2}$.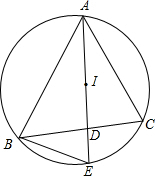 如图,点I是△ABC的内心,AI的延长线交边BC于点D,交△ABC外接圆于点E.
如图,点I是△ABC的内心,AI的延长线交边BC于点D,交△ABC外接圆于点E.