题目内容
4.已知等腰三角形△ABC,有一个角是80°,其它两个角是80°,20°或50°,50°.分析 等腰三角形有一个内角为80°,80°没有明确是顶角还是底角,故分两种情况考虑:若80°为顶角时,根据等腰三角形的两底角相等,利用三角形内角和定理求出两底角即为另两内角;若80°为底角,根据等腰三角形的两底角相等,可得出另外一个底角也为80°,利用三角形内角和定理求出顶角,进而得到另两个内角.
解答 解:若80°为顶角时,根据等腰三角形的性质及内角和定理可得:
底角为$\frac{1}{2}$(180°-80°)=50°,故另两内角为:50°,50°;
若80°为底角,根据等腰三角形的两底角相等,可得出另外一个底角也为80°,
则顶角为:180°-80°-80°=20°,故另两内角为:80°,20°,
综上,另两内角为:80°,20°或50°,50°.
故答案为:80°,20°或50°,50°.
点评 此题考查了等腰三角形的性质,以及三角形的内角和定理,有关腰长与底边、顶角与底角、腰上的高等问题,要注意分类讨论,不要漏解.此类型题是中考中的基本题型.

练习册系列答案
相关题目
19.在数-27,-1.25,0,$\frac{24}{7}$中,立方根为正数的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
9.下列实数是无理数的是( )
| A. | -2 | B. | 0 | C. | $\frac{1}{3}$ | D. | $\sqrt{3}$ |
13.下列式子中,最简二次根式是( )
| A. | $\sqrt{5{x}^{3}}$ | B. | $\sqrt{4m}$ | C. | $\sqrt{{a}^{2}+3}$ | D. | $\sqrt{\frac{1}{x}}$ |
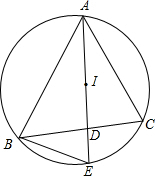 如图,点I是△ABC的内心,AI的延长线交边BC于点D,交△ABC外接圆于点E.
如图,点I是△ABC的内心,AI的延长线交边BC于点D,交△ABC外接圆于点E. 如图是由5个大小相同的小正方体搭成的几何体,它的左视图是( )
如图是由5个大小相同的小正方体搭成的几何体,它的左视图是( )


