题目内容
19.先化简,再求($\frac{a+b}{a-b}$+$\frac{a}{b-a}$)÷$\frac{{b}^{2}}{{a}^{2}-ab}$的值,且a、b满足|a-$\sqrt{3}$|+$\sqrt{b+1}$=0.分析 先化简原式,然后将a与b的值代入即可求出答案.
解答 解:原式=$(\frac{a+b}{a-b}-\frac{a}{a-b})×\frac{a(a-b)}{b^2}$
=$\frac{b}{a-b}×\frac{a(a-b)}{b^2}$
=$\frac{a}{b}$
∵$|{a-\sqrt{3}}|+\sqrt{b+1}=0$
∴$a=\sqrt{3}$,b=-1
∴原式=$\frac{a}{b}=\frac{{\sqrt{3}}}{-1}=-\sqrt{3}$
点评 本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
相关题目
9.北盘江旅游景点在2017年6月4日至6月14日蓄水期间,水位由106米直升至135米,是划船旅游最佳的时期,设水位匀速上生,那么下列图象中,能反应这10天水位h(米)随时间t(天)变化的是( )
| A. |  | B. | 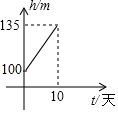 | C. | 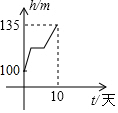 | D. | 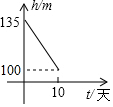 |
14.据报道,目前我国“天河二号”超级计算机的运算速度位居全球第一,其运算速度达到了每秒338 600 000亿次,数字338 600 000用科学记数法(保留3个有效数字)可简洁表示为( )
| A. | 3.4×108 | B. | 0.34×109 | C. | 3.38×108 | D. | 3.39×108 |
11. 三个正方形的面积如图,正方形A的面积为( )
三个正方形的面积如图,正方形A的面积为( )
 三个正方形的面积如图,正方形A的面积为( )
三个正方形的面积如图,正方形A的面积为( )| A. | 6 | B. | 4 | C. | 64 | D. | 8 |
8.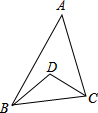 如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB角平分线的交点,则∠BDC=( )
如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB角平分线的交点,则∠BDC=( )
 如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB角平分线的交点,则∠BDC=( )
如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB角平分线的交点,则∠BDC=( )| A. | 110° | B. | 100° | C. | 90° | D. | 80° |
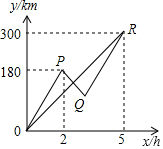 已知A,B两地公路长300km,甲、乙两车同时从A地出发沿同一公路驶往B地,2小时后,甲车接到电话需返回这条公路上的C处取回货物,于是甲车立即原路返回C,取了货物又立即赶往B地(取货物的时间忽略不计),结果两车同时到达B地.两车的速度始终保持不变,设两车出发x小时后,甲、乙距离A地的距离分别为y1(km)和y2(km),它们的函数图象分别是折线OPQR和线段OR.
已知A,B两地公路长300km,甲、乙两车同时从A地出发沿同一公路驶往B地,2小时后,甲车接到电话需返回这条公路上的C处取回货物,于是甲车立即原路返回C,取了货物又立即赶往B地(取货物的时间忽略不计),结果两车同时到达B地.两车的速度始终保持不变,设两车出发x小时后,甲、乙距离A地的距离分别为y1(km)和y2(km),它们的函数图象分别是折线OPQR和线段OR.