题目内容
19.等腰三角形的两边长为10,12,则顶角的正弦值是$\frac{24}{25}$或$\frac{5}{72}$$\sqrt{119}$.分析 分两种情况:腰长为4,底边为6;腰长为6,底边为4.分别求底边上的高,运用三角函数定义求解.
解答 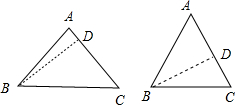 解:分两种情况解答.
解:分两种情况解答.
(1)腰长为10,底边为12.
设AD=x,则CD=10-x,
由勾股定理可知:102-x2=122-(10-x)2,
解得x=$\frac{14}{5}$,
∴AD=$\frac{14}{5}$,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\frac{48}{5}$
∴sinA=$\frac{BD}{AB}$=$\frac{24}{25}$;
(2)腰长为12,底边为10.
同理求得AD=$\frac{47}{6}$,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\frac{5\sqrt{119}}{6}$
∴sinA=$\frac{BD}{AB}$=$\frac{5}{72}$$\sqrt{119}$
故答案为$\frac{24}{25}$或$\frac{5}{72}$$\sqrt{119}$.
点评 此题主要考查了等腰三角形的性质,解直角三角形以及三角函数的定义和分类讨论的思想方法.

练习册系列答案
相关题目
7.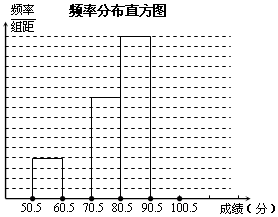 为了让学生了解环保知识,增强环保意识.某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频数分布表和频数分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识.某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频数分布表和频数分布直方图,解答下列问题:
频数分布表
(1)频数分布表中a=12;b=50;
(2)补全频数分布直方图;(3)在该问题中的样本容量是50;
(4)全体参赛学生中,竞赛成绩落在80.5~90.5组范围内的人数最多;
(5)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为216人.
 为了让学生了解环保知识,增强环保意识.某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频数分布表和频数分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识.某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频数分布表和频数分布直方图,解答下列问题:频数分布表
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 008 |
| 60.5~70.5 | 8 | b |
| 70.5~80.5 | 10 | 020 |
| 80.5~90.5 | 16 | 032 |
| 90.5~100.5 | a | 0.24 |
| 合计 |
(2)补全频数分布直方图;(3)在该问题中的样本容量是50;
(4)全体参赛学生中,竞赛成绩落在80.5~90.5组范围内的人数最多;
(5)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为216人.
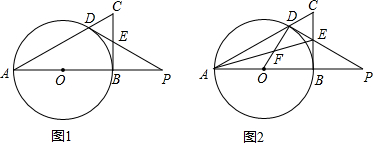
 如图,直线a∥b,∠1=70°,∠2=35°,则∠3的度数是35°.
如图,直线a∥b,∠1=70°,∠2=35°,则∠3的度数是35°.