题目内容
19．先化简，再求值：（1+$\frac{1}{x-2}$）÷$\frac{x-1}{{x}^{2}-4x+4}$，其中x=3．分析 根据分式的加法和除法可以化简题目中的式子，然后将x的值代入化简后的式子即可解答本题．
解答 解：（1+$\frac{1}{x-2}$）÷$\frac{x-1}{{x}^{2}-4x+4}$
=$\frac{x-2+1}{x-2}•\frac{（x-2）^{2}}{x-1}$
=$\frac{（x-1）（x-2）}{x-1}$
=x-2，
当x=3时，原式=3-2=1．
点评 本题考查分式的化简求值，解答本题的关键是明确分式化简求值的方法．
练习册系列答案
相关题目
14．把抛物线y=-x2向右平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为（ ）
| A． | y=-（x-1）2-3 | B． | y=-（x+1）2-3 | C． | y=-（x-1）2+3 | D． | y=-（x+1）2+3 |
如图，在△ABC中，D、E分别是边AB、AC的中点，则△ADE与△ABC的面积比S△ADE：S△ABC=1：4．
如图是由若干小正方体组成的几何体的俯视图，小正方形中的数字表示该位置小正方体的个数，这个几何体的主视图是（ ）
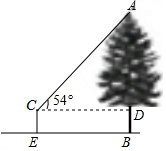如图，创新小组要测量公园内一棵树的高度AB，其中一名小组成员站在距离树10米的点E处，测得树顶A的仰角为54°．已知测角仪的架高CE=1.5米，则这棵树的高度为15.3米．（结果保留一位小数．参考数据：sin54°=0.8090，cos54°=0.5878，tan54°=1.3764）