题目内容
1.计算:(1)$\root{3}{1+\frac{61}{64}}$;
(2)-$\root{3}{\frac{7}{8}-1}$;
(3)$\sqrt{\frac{4}{9}}$÷$\sqrt{\frac{25}{81}}$-$\root{3}{-0.027}$×$\root{3}{\frac{125}{216}}$;
(4)$\frac{1}{3}$$\sqrt{144}$-5×$\root{3}{0.008}$.
分析 (1)先算根号内的加法,再计算立方根;
(2)先算根号内的减法,再计算立方根;
(3)先算根号,再算乘除法,最后计算减法;
(4)先算根号,再算乘法,最后计算减法.
解答 解:(1)$\root{3}{1+\frac{61}{64}}$=$\root{3}{\frac{125}{64}}$=$\frac{5}{4}$;
(2)-$\root{3}{\frac{7}{8}-1}$=-$\root{3}{-\frac{1}{8}}$=$\frac{1}{2}$;
(3)$\sqrt{\frac{4}{9}}$÷$\sqrt{\frac{25}{81}}$-$\root{3}{-0.027}$×$\root{3}{\frac{125}{216}}$
=$\frac{2}{3}$÷$\frac{5}{9}$-(-0.3)×$\frac{5}{6}$
=$\frac{6}{5}$+$\frac{1}{2}$
=$\frac{17}{10}$;
(4)$\frac{1}{3}$$\sqrt{144}$-5×$\root{3}{0.008}$
=$\frac{1}{3}$×12-5×0.2
=4-1
=3.
点评 本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握二次根式、三次根式等考点的运算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.如图,∠AED和∠BDE是( )


| A. | 同位角 | B. | 内错角 | C. | 同旁内角 | D. | 互为补角 |
9.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16.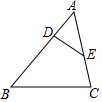 如图,△ABC中,D、E分别在AB、AC上,下列条件中不能判断△ADE∽△ACB的是( )
如图,△ABC中,D、E分别在AB、AC上,下列条件中不能判断△ADE∽△ACB的是( )
 如图,△ABC中,D、E分别在AB、AC上,下列条件中不能判断△ADE∽△ACB的是( )
如图,△ABC中,D、E分别在AB、AC上,下列条件中不能判断△ADE∽△ACB的是( )| A. | ∠ADE=∠C | B. | ∠AED=∠B | C. | $\frac{AD}{AC}=\frac{AE}{AB}$ | D. | $\frac{AD}{AC}=\frac{DE}{BC}$ |
6.在平面直角坐标系中,点P在x轴上方,且点P到x轴的距离为2,到y轴的距离为3,则点P的坐标为( )
| A. | (2,3) | B. | (3,2) | C. | (-3,2)或(3,2) | D. | (-2,3)或(2,3) |
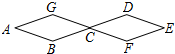 如图,两个完全相同的菱形其边长为1厘米,一只蚂蚁由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,行走2017厘米后停下,则这只蚂蚁停在B点.
如图,两个完全相同的菱形其边长为1厘米,一只蚂蚁由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,行走2017厘米后停下,则这只蚂蚁停在B点.