题目内容
16.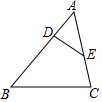 如图,△ABC中,D、E分别在AB、AC上,下列条件中不能判断△ADE∽△ACB的是( )
如图,△ABC中,D、E分别在AB、AC上,下列条件中不能判断△ADE∽△ACB的是( )| A. | ∠ADE=∠C | B. | ∠AED=∠B | C. | $\frac{AD}{AC}=\frac{AE}{AB}$ | D. | $\frac{AD}{AC}=\frac{DE}{BC}$ |
分析 A和B:根据有两组角对应相等的两个三角形相似,进行判断即可;
C、根据两组对应边的比相等且夹角对应相等的两个三角形相似,进行判断即可;
D、根据两组对应边的比相等且夹角对应相等的两个三角形相似,进行判断即可.
解答 解:A、由∠ADE=∠C,∠A=∠A,则可判断△ADE∽△ACB;
B、由∠AED=∠B,∠A=∠A,则可判断△ADE∽△ACB;
C、由$\frac{AD}{AC}=\frac{AE}{AB}$,∠A=∠A,则可判断△ADE∽△ACB;
D、因为$\frac{AD}{AC}=\frac{DE}{BC}$,此时不确定∠ADE=∠ACB,故不能确定△ADE∽△ACB;
因为本题选择不能判断△ADE∽△ACB的条件,
故选:D.
点评 此题考查了相似三角形的判定,属于基础题,关键是掌握相似三角形的三种判定定理.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
6.男生小明和三名女生、四名男生一起玩丢手帕游戏,小明随意将手帕丢在一名同学的后面,那么这名同学是女生的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{8}$ | C. | $\frac{3}{7}$ | D. | 无法确定 |
7.若分式$\frac{x+2}{x-3}$的值为零,则( )
| A. | x=3 | B. | x=-3 | C. | x=2 | D. | x=-2 |
4.在下列实数$\frac{7}{3}$,π-3.14,3.14,$\sqrt{12}$,0.2$\stackrel{•}{2}$,$\sqrt{9}$中无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.下列二次根式中,与$\sqrt{3}$不是同类二次根式的是( )
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\sqrt{6}$ | C. | $\sqrt{12}$ | D. | $\sqrt{27}$ |
8. 将一副直角三角板如图放置,则∠1的度数为( )
将一副直角三角板如图放置,则∠1的度数为( )
 将一副直角三角板如图放置,则∠1的度数为( )
将一副直角三角板如图放置,则∠1的度数为( )| A. | 75° | B. | 65° | C. | 45° | D. | 30° |
5.下列命题中,是真命题的是( )
| A. | 一个角的余角大于这个角 | B. | 邻补角一定互补 | ||
| C. | 相等的角是对顶角 | D. | 有且只有一条直线与已知直线垂直 |
6.下列各组数中,不是二元一次方程x+y=10的一组解的是( )
| A. | $\left\{{\begin{array}{l}{x=-3}\\{y=13}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x=12}\\{y=-2}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{x=2}\\{y=5}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{x=4}\\{y=6}\end{array}}\right.$ |