题目内容

12．一个六边形的六边长分别为3，4，5，6，7，8，另一个与其相似的六边形的周长为66，则与其相似的六边形的最短边为6．

分析 设另一个六边形的最短边的长为x，根据相似多边形的性质得$\frac{x}{3}$=$\frac{66}{3+4+5+6+7+8}$，然后解关于x的方程即可．

解答 解：设另一个六边形的最短边的长为x，
根据题意得$\frac{x}{3}$=$\frac{66}{3+4+5+6+7+8}$，
解得x=6，
即另一个六边形的最短边的长为6．
故答案为6．

点评 本题考查了相似多边形的性质：对应角相等；对应边的比相等．

练习册系列答案
相关题目
2．对于不等式2x＞-4，下列解集正确的是（　　）
A．x＞2B．x＞-2C．x＜-2D．x＞-$\frac{1}{2}$
3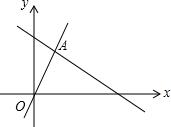．如图，函数y=2x和y=ax+1的图象相交于A（m，3），则不等式2x＜ax+1的解集为（　　）
A．x＜$\frac{3}{2}$B．x＜3C．x＞$\frac{3}{2}$D．x＞3
20．如图，四边形ABCD是平行四边形，则下列结论：①若AB=BC，则四边形ABCD一定是菱形；②若AC⊥BD，则四边形ABCD一定是矩形；③若∠ABC=90°，则四边形ABCD一定是菱形；④若AC=BD，则四边形ABCD一定是正方形．其中正确的有（　　）
A．1个B．2个C．3个D．4个
7．若分式$\frac{x+2}{x-3}$的值为零，则（　　）
A．x=3B．x=-3C．x=2D．x=-2
17．某种服装的进价为240元，出售时标价为330元，由于换季，商店准备打折销售，但要保持利润不低于10%，那么至多打（　　）
A．6折B．7折C．8折D．9折
4．在下列实数$\frac{7}{3}$，π-3.14，3.14，$\sqrt{12}$，0.2$\stackrel{•}{2}$，$\sqrt{9}$中无理数有（　　）
A．1个B．2个C．3个D．4个
1．计算：
（1）$\root{3}{1+\frac{61}{64}}$；
（2）-$\root{3}{\frac{7}{8}-1}$；
（3）$\sqrt{\frac{4}{9}}$÷$\sqrt{\frac{25}{81}}$-$\root{3}{-0.027}$×$\root{3}{\frac{125}{216}}$；
（4）$\frac{1}{3}$$\sqrt{144}$-5×$\root{3}{0.008}$．
2．下列从左边到右边的变形，属于因式分解的是（　　）
A．（3-x）（3+x）=9-x2B．（y+1）（y-3）=-（3-y）（y+1）
C．m4-n4=（m2+n2）（m+n）（m-n）D．4yz-2y2z+z=2y（2z-yz）+z

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网