题目内容
18.正六边形的边长为2,则它的面积为( )| A. | $\frac{3\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
分析 构建等边三角形,由题意可得:正六边形的面积就是6个等边△OCD的面积,根据边长为2求得三角形的高线OG=$\sqrt{3}$,代入面积公式计算即可.
解答 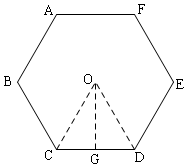 解:如图,设正六边形ABCDEF的中心为O,连接OC、OD,
解:如图,设正六边形ABCDEF的中心为O,连接OC、OD,
过O作OG⊥CD于G,
∵∠COD=$\frac{360}{6}$=60°,OC=OD,
∴△COD是等边三角形,
∴OC=CD=OD=2,
∴CG=DG=1,
由勾股定理得:OG=$\sqrt{3}$,
∴S正六边形ABCDEF=6S△OCD=6×$\frac{1}{2}$×CD×OG=3×2×$\sqrt{3}$=6$\sqrt{3}$,
故选D.
点评 本题考查了正六边形的性质及三角形的面积,正确计算中心角的度数=$\frac{360}{边数}$,熟知半径与边长构成等边三角形,求正六边形的面积,其实就是求等边三角形的面积.

练习册系列答案
相关题目
9.下列各式,分解因式正确的是( )
| A. | a2-b2=(a-b)2 | B. | a2-2ab+b2-1=(a-b+1)(a-b-1) | ||
| C. | x3y-4xy=xy(x2-4) | D. | xy+xz+x=x(y+z) |
6.已知x=5是方程ax+4=16-a的解,则a的值是( )
| A. | -2 | B. | 2 | C. | 5 | D. | -5 |
13.方程x2=2017x的解是( )
| A. | x=0 | B. | x=1 | C. | x=2017 | D. | x=0或2017 |
10.将抛物线y=$\frac{1}{2}$x2+1向左平移2个单位,再向下平移3个单位,得到的抛物线的函数表达式为( )
| A. | y=$\frac{1}{2}$(x-2)2+4 | B. | y=$\frac{1}{2}$(x-2)2-2 | C. | y=$\frac{1}{2}$(x+2)2+4 | D. | y=$\frac{1}{2}$(x+2)2-2 |
 如图是正方体的展开图,若约定用字母S表示正方体的侧面,用T表示上面,A表示底面,则字母A在展开图中的位置是( )
如图是正方体的展开图,若约定用字母S表示正方体的侧面,用T表示上面,A表示底面,则字母A在展开图中的位置是( )