题目内容
已知点A、B、C在⊙O上,若AB=AC,BC=24,⊙O半径为13,则△ABC的BC边上的高为 .
考点:垂径定理,勾股定理
专题:分类讨论
分析:分点A在优弧和劣弧上两种情况,当A在优弧上时,过A作AD⊥BC于点D,则可知O在AD上,连接BD,在Rt△BOD中可求得OD=5,可知AD=5+13,当点A在劣弧上时可知AD=OA-AD=8.
解答:解:如图1,当点A在优弧上时,过A作AD⊥BC于点D,

∵AB=AC,
∴BD=CD=12,且圆心O在AD上,
连接OB,则OB=OA=13,
在Rt△BOD中,由勾股定理可求得OD=5,
∴AD=AO+OD=13+5=18;
如图2,当点A在劣弧上时,过A作AD⊥BC于点D,

∵AB=AC,
∴BD=CD=12,且圆心O在AD上,
连接OB,则OB=OA=13,
在Rt△BOD中,由勾股定理可求得OD=5,
∴AD=AO-OD=13-5=8;
综上可知△ABC的BC边上的高为8或18,
故答案为:8或18.

∵AB=AC,
∴BD=CD=12,且圆心O在AD上,
连接OB,则OB=OA=13,
在Rt△BOD中,由勾股定理可求得OD=5,
∴AD=AO+OD=13+5=18;
如图2,当点A在劣弧上时,过A作AD⊥BC于点D,

∵AB=AC,
∴BD=CD=12,且圆心O在AD上,
连接OB,则OB=OA=13,
在Rt△BOD中,由勾股定理可求得OD=5,
∴AD=AO-OD=13-5=8;
综上可知△ABC的BC边上的高为8或18,
故答案为:8或18.
点评:本题主要考查垂径定理和等腰三角形的性质、勾股定理等知识的应用,分点A在优弧和劣弧上两种情况求解是解题的关键.注意勾股定理的应用.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 画出图中无盖正方体纸盒的一种表面展开图.
画出图中无盖正方体纸盒的一种表面展开图. 东海中有某一小岛上有一灯塔A,已知灯塔附近方圆25海里范围内有暗礁,我军110舰在O点处测得灯塔在北偏西60°方向,向正西方向航行20海里后到达B处,侧得灯塔在西北方向,如果该舰继续向西航行,是否有触礁危险?请说明理由.
东海中有某一小岛上有一灯塔A,已知灯塔附近方圆25海里范围内有暗礁,我军110舰在O点处测得灯塔在北偏西60°方向,向正西方向航行20海里后到达B处,侧得灯塔在西北方向,如果该舰继续向西航行,是否有触礁危险?请说明理由.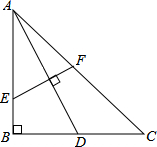 如图,已知在△ABC中,∠B=90°,AB=BC,AD是BC边上的中线,EF是AD的垂直平分线,交AB于点E,交AC于点F,求AE:BE的值.
如图,已知在△ABC中,∠B=90°,AB=BC,AD是BC边上的中线,EF是AD的垂直平分线,交AB于点E,交AC于点F,求AE:BE的值. 如图,△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为
如图,△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为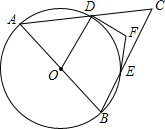 如图,点C为以AB为直径的⊙O外一点,AC、BC分别交⊙O于点D、E,DF、EF为⊙O的切线,已知∠ACB=64°,则∠DFE
如图,点C为以AB为直径的⊙O外一点,AC、BC分别交⊙O于点D、E,DF、EF为⊙O的切线,已知∠ACB=64°,则∠DFE