题目内容
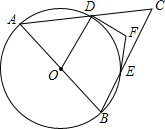 如图,点C为以AB为直径的⊙O外一点,AC、BC分别交⊙O于点D、E,DF、EF为⊙O的切线,已知∠ACB=64°,则∠DFE
如图,点C为以AB为直径的⊙O外一点,AC、BC分别交⊙O于点D、E,DF、EF为⊙O的切线,已知∠ACB=64°,则∠DFE考点:切线的性质
专题:
分析:如图,作辅助线,首先证明∠DFE=360°-2(α+β);进而求出α+β=180°-64°=116°,问题即可解决.
解答: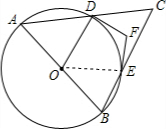 解:连接OE,
解:连接OE,
∵DF、EF分别为⊙O的切线,
∴∠OEF=∠ODF=90°,
∴∠DFE=180°-∠DOE;
∵OA=OD,OB=OE,
∴∠A=∠ODA(设为α),∠B=∠OEB(设为β);
∴∠AOD+∠BOE=180°-2α+180°-2β
=360°-2(α+β),
而∠AOD+∠BOE=180°-∠DOE,
∴∠DFE=360°-2(α+β);
∵∠C=64°,
∴α+β=180°-64°=116°,
∴∠DFE=360°-232°=128°,
即∠DFE的度数为128°.
 解:连接OE,
解:连接OE,∵DF、EF分别为⊙O的切线,
∴∠OEF=∠ODF=90°,
∴∠DFE=180°-∠DOE;
∵OA=OD,OB=OE,
∴∠A=∠ODA(设为α),∠B=∠OEB(设为β);
∴∠AOD+∠BOE=180°-2α+180°-2β
=360°-2(α+β),
而∠AOD+∠BOE=180°-∠DOE,
∴∠DFE=360°-2(α+β);
∵∠C=64°,
∴α+β=180°-64°=116°,
∴∠DFE=360°-232°=128°,
即∠DFE的度数为128°.
点评:该命题以圆为载体,在考查圆的切线的性质及其应用的同时,还考查了三角形的内角和定理等几何知识点;灵活运用有关定理来解题是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 请你把五个数+(-3),(-2)2,|-2.5|,0,-(+1.5)表示在图1数轴上,并按从小到大顺序,从左到右串个糖葫芦,把数填在图2“○”内.
请你把五个数+(-3),(-2)2,|-2.5|,0,-(+1.5)表示在图1数轴上,并按从小到大顺序,从左到右串个糖葫芦,把数填在图2“○”内.