题目内容
1．
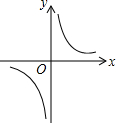已知反比例函数y=$\frac{ab}{x}$（ab≠0）的图象如图所示，则二次函数y=ax2+bx-2的大致图象是（ ）| A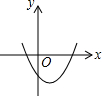． |  | B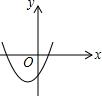． |  | C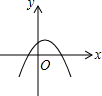． |  | D． |  |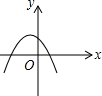
分析 先根据反比例函数图象得到a、b同号，再根二次函数图象与系数的关系以及对称轴的位置判断正确选项．
解答 解：∵反比例函数图象在一三象限，
∴ab＞0，
∴a、b同号，
∴抛物线对称轴x=-$\frac{b}{2a}$＜0，
∵二次函数y=ax2+bx-2
∴抛物线交y轴的负半轴，
∴只有选项B符号，
故选：B．
点评 本题考查了二次函数的图象：二次函数y=ax2+bx+c（a、b、c为常数，a≠0）的图象为抛物线，当a＞0，抛物线开口向上；当a＜0，抛物线开口向下．对称轴为直线x=-$\frac{b}{2a}$；与y轴的交点坐标为（0，c）．也考查了反比例函数的图象．
练习册系列答案
相关题目
11．若多项式4x2-kxy+y2是完全平方式，则k的值是（ ）
| A． | 4 | B． | ±4 | C． | -4 | D． | 2 |
9．
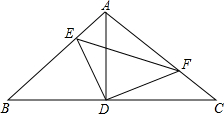如图，Rt△ABC中，∠BAC=90°，AB=AC，点D为BC的中点，点E、F分别在边AB和边AC上，且∠EDF=90°，则下列结论不一定成立的是（ ）
如图，Rt△ABC中，∠BAC=90°，AB=AC，点D为BC的中点，点E、F分别在边AB和边AC上，且∠EDF=90°，则下列结论不一定成立的是（ ）| A． | △ADF≌△BDE | B． | S四边形AEDF=$\frac{1}{2}$S△ABC | ||
| C． | BE+CF=$\sqrt{2}$AD | D． | EF=AD |
16．下列函数关系式中，表示y是x的反比例函数的是（ ）
| A． | y=$\frac{1}{{x}^{2}}$ | B． | y=$\sqrt{2}$x | C． | y=$\frac{5}{x}$ | D． | y=$\frac{x}{3}$ |
6．
长方形纸片ABCD中，E为AD边上一点，将纸片沿BE折叠后，点A落在CD边上F点，若∠CBF=∠EBF，则∠DEF的度数为（ ）
长方形纸片ABCD中，E为AD边上一点，将纸片沿BE折叠后，点A落在CD边上F点，若∠CBF=∠EBF，则∠DEF的度数为（ ）| A． | 15° | B． | 30° | C． | 45° | D． | 60° |
13．
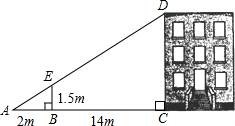如图，利用标杆BE测量建筑物的高度，标杆BE高1.5m，测得AB=2m，BC=14m，则楼高CD为（ ）
如图，利用标杆BE测量建筑物的高度，标杆BE高1.5m，测得AB=2m，BC=14m，则楼高CD为（ ）| A． | 10.5m | B． | 9.5m | C． | 12m | D． | 14m |
10．在-12，|-5|，-（-4），-|0|中，正数共有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
11．
如图，在△ABC中，∠B=90°，∠A=60°，AB=4，则AC的长度为（ ）
如图，在△ABC中，∠B=90°，∠A=60°，AB=4，则AC的长度为（ ）| A． | 4 | B． | 6 | C． | 8 | D． | 10 |