题目内容
对于抛物线y=x2+bx+c,给出以下陈述:
①它的对称轴为x=2;
②它与x轴有两个交点为A、B;
③△APB的面积不小于27(P为抛物线的顶点).
求①、②、③得以同时成立时,常数b、c的取值范围.
①它的对称轴为x=2;
②它与x轴有两个交点为A、B;
③△APB的面积不小于27(P为抛物线的顶点).
求①、②、③得以同时成立时,常数b、c的取值范围.
考点:二次函数图象与系数的关系
专题:
分析:①它的对称轴为x=2,则由对称轴公式得到b的值;
②它与x轴有两个交点为A、B,则根的判别式△>0;
③△APB的面积不小于27(P为抛物线的顶点),则根据根与系数的关系、抛物线顶点坐标公式求得关于c的不等式,由此可以求得c的取值范围.
②它与x轴有两个交点为A、B,则根的判别式△>0;
③△APB的面积不小于27(P为抛物线的顶点),则根据根与系数的关系、抛物线顶点坐标公式求得关于c的不等式,由此可以求得c的取值范围.
解答:解:∵抛物线y=x2+bx+c=(x+
)2+
,抛物线y=x2+bx+c的对称轴为x=2,
∴-
=2,则b=-4,
∴P点的纵坐标是
=c-4,
又∵它与x轴有两个交点为A、B,
∴△=b2-4ac=16-4c>0,且AB=
=
=2
解得 c<
,①
又△APB的面积不小于27,
∴
×2
×|c-16|≥27,即
×|c-16|≥27②
由①②解得 c≤-5.
综上所述,b的值是-4,c的取值范围是c≤-5.
| b |
| 2 |
| 4c-b2 |
| 4 |
∴-
| b |
| 2 |
∴P点的纵坐标是
| 4c-b2 |
| 4 |
又∵它与x轴有两个交点为A、B,
∴△=b2-4ac=16-4c>0,且AB=
| b2-4c |
| 16-4c |
| 4-c |
解得 c<
| 1 |
| 4 |
又△APB的面积不小于27,
∴
| 1 |
| 2 |
| 4-c |
| 4-c |
由①②解得 c≤-5.
综上所述,b的值是-4,c的取值范围是c≤-5.
点评:本题考查了二次函数图象与系数的关系、抛物线与x轴的交点.熟记抛物线顶点坐标公式是解题的关键.

练习册系列答案
相关题目
已知OA是⊙O的半径,若CD⊥OA,则以下说法正确的是( )
| A、CD⊙O的切线 |
| B、CD与⊙O相离 |
| C、CD与⊙O相切 |
| D、不能确定 |
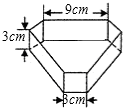 如图所示,是一种“口子窖”酒的包装纸盒,它的侧面由长方形和正方形组成.经测量,底面六变形有三条边的长是9cm,有三条边的长是3cm,每个内角都是120°,该六棱柱的高是3cm,请你设计一种裁剪方案,使之能制作这种无盖的包装盒.
如图所示,是一种“口子窖”酒的包装纸盒,它的侧面由长方形和正方形组成.经测量,底面六变形有三条边的长是9cm,有三条边的长是3cm,每个内角都是120°,该六棱柱的高是3cm,请你设计一种裁剪方案,使之能制作这种无盖的包装盒.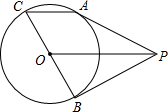 已知,如图,点P在⊙O外,PA、PB是⊙O的切线,A、B为切点,BC是直径,连接CA.求证:CA∥OP.
已知,如图,点P在⊙O外,PA、PB是⊙O的切线,A、B为切点,BC是直径,连接CA.求证:CA∥OP.