题目内容
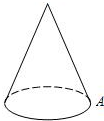 如图,地面半径为1,母线长为4的圆锥A处有一只蚂蚁,它绕这个圆锥侧面爬行一圈后回到A处,则蚂蚁所走最短路线长为( )
如图,地面半径为1,母线长为4的圆锥A处有一只蚂蚁,它绕这个圆锥侧面爬行一圈后回到A处,则蚂蚁所走最短路线长为( )| A、2 | ||
B、4
| ||
C、4
| ||
| D、4 |
考点:平面展开-最短路径问题,圆锥的计算
专题:
分析:要求蚂蚁爬行的最短距离,需将圆锥的侧面展开,进而根据“两点之间线段最短”得出结果.
解答: 解:∵底面圆的半径为1,
解:∵底面圆的半径为1,
∴底面周长等于2π.
设圆锥的侧面展开后的扇形圆心角为n°,则2π=
,
解得n=90°,
∴展开图中圆心角为90°,
∴AA′=
=
=4
.
故选B.
 解:∵底面圆的半径为1,
解:∵底面圆的半径为1,∴底面周长等于2π.
设圆锥的侧面展开后的扇形圆心角为n°,则2π=
| 4nπ |
| 180 |
解得n=90°,
∴展开图中圆心角为90°,
∴AA′=
| 16+16 |
| 32 |
| 2 |
故选B.
点评:本题考查的是平面展开-最短路径问题,此类问题应先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.

练习册系列答案
相关题目
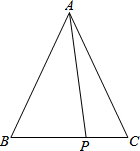 如图,在△ABC中,AB=AC=5,P是BC边上除B、C点外的任意一点,则代数式AP2+PB•PC等于( )
如图,在△ABC中,AB=AC=5,P是BC边上除B、C点外的任意一点,则代数式AP2+PB•PC等于( )| A、25 | B、15 | C、20 | D、30 |
下列四个角中,最有可能与60°角互补的是( )
A、 |
B、 |
C、 |
D、 |
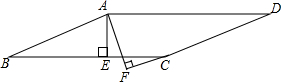 如图所示,在?ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6,S?ABCD=72,则?ABCD的周长是( )
如图所示,在?ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6,S?ABCD=72,则?ABCD的周长是( )| A、64 | B、60 | C、70 | D、56 |
 如图,正六边形ABCDEF的边长为R,分别以点C、F为圆心,R为半径画弧,则图中阴影部分的弧长为
如图,正六边形ABCDEF的边长为R,分别以点C、F为圆心,R为半径画弧,则图中阴影部分的弧长为 “三角板”是大家常见的,你思考过“三角板”中蕴含的数学问题吗?下面老师随意编一题请大家算算:
“三角板”是大家常见的,你思考过“三角板”中蕴含的数学问题吗?下面老师随意编一题请大家算算: