题目内容
“三角板”是大家常见的，你思考过“三角板”中蕴含的数学问题吗？下面老师随意编一题请大家算算：如图，若教师用的含30°角的三角板每条边的板宽为3cm，外框斜边AB=60cm，我们知道内、外框两个三角形是相似的，则内、外框两个三角形的相似比为
考点：相似三角形的应用
专题：
分析：连接AD，作DM⊥AC于M，FN⊥AC于N，即可求得MN的长，从而求得内、外框两个三角形的相似比．
解答：
解：连接AD，作DM⊥AC于M，FN⊥AC于N，则DM=FN=3cm．
∵直角△ABC中，∠ABC=30°，
∴AC=
AB=
×60=30cm．
∵D到AB与到AC的距离相等，
∴AD平分∠BAC，
∴∠DAM=30°，
∴AM=
DM=3
cm，
同理CN=FN=3cm，
∴DF=MN=AC-AM-CN=30-3
-3=27-3
，
∴内、外框两个三角形的相似比为
=
=
．
故答案是：
．
解：连接AD，作DM⊥AC于M，FN⊥AC于N，则DM=FN=3cm．∵直角△ABC中，∠ABC=30°，
∴AC=
| 1 |
| 2 |
| 1 |
| 2 |
∵D到AB与到AC的距离相等，
∴AD平分∠BAC，
∴∠DAM=30°，
∴AM=
| 3 |
| 3 |
同理CN=FN=3cm，
∴DF=MN=AC-AM-CN=30-3
| 3 |
| 3 |
∴内、外框两个三角形的相似比为
| DF |
| AC |
27-3
| ||
| 30 |
9-
| ||
| 10 |
故答案是：
9-
| ||
| 10 |
点评：本题考查了相似三角形的应用，含30°角的直角三角形的性质，角平分线的判定，关键是作出辅助线求得MN的长．
练习册系列答案
相关题目
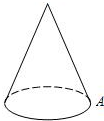如图，地面半径为1，母线长为4的圆锥A处有一只蚂蚁，它绕这个圆锥侧面爬行一圈后回到A处，则蚂蚁所走最短路线长为（ ）| A、2 | ||
B、4
| ||
C、4
| ||
| D、4 |
下列各式：y=2x2-3xz+5； y=3-2x+5x2； y=x2+2x-3； y=ax2+bx+c； y=（2x-3）（3x-2）-6x2； y=（m2+1）x2+3x-4； y=m2x2+4x-3． 是二次函数的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
下列函数，为反比例函数的是（ ）
A、y=-
| ||
B、y=-
| ||
C、y=x+
| ||
D、y=-x2+
|
各式中，分式的个数有（ ）
x+
y，
，
，-4xy，
，
．
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| xy |
| 1 |
| 5+a |
| x |
| x2 |
| x |
| π |
| A、1个 | B、2个 | C、3个 | D、4个 |
如图，△ABC中∠ABC=∠ACB，AB的垂直平分线交AC于点D．若∠A=40°，则∠DBC=