题目内容
Rt△ABC中,BC=8,AC=15,∠C=90°,则AB= .
考点:勾股定理
专题:
分析:在Rt△ABC中,利用勾股定理可求出AB的长度.
解答: 解:∵∠C=90°,BC=8,AC=15,
解:∵∠C=90°,BC=8,AC=15,
∴AB=
=
=17;
故答案为:17.
 解:∵∠C=90°,BC=8,AC=15,
解:∵∠C=90°,BC=8,AC=15,∴AB=
| AC2+BC2 |
| 152+82 |
故答案为:17.
点评:此题考查了勾股定理的知识,属于基础题,掌握勾股定理的形式是关键.

练习册系列答案
相关题目
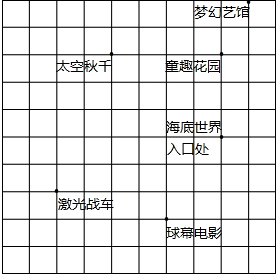 如图是“欢欢游乐城”的平面示意图,如果用(8,5)表示入口处的位置,那么(8,8)表示的位置是( )
如图是“欢欢游乐城”的平面示意图,如果用(8,5)表示入口处的位置,那么(8,8)表示的位置是( )| A、太空秋千 | B、梦幻艺馆 |
| C、童趣花园 | D、球幕电影 |
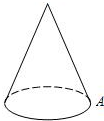 如图,地面半径为1,母线长为4的圆锥A处有一只蚂蚁,它绕这个圆锥侧面爬行一圈后回到A处,则蚂蚁所走最短路线长为( )
如图,地面半径为1,母线长为4的圆锥A处有一只蚂蚁,它绕这个圆锥侧面爬行一圈后回到A处,则蚂蚁所走最短路线长为( )| A、2 | ||
B、4
| ||
C、4
| ||
| D、4 |
将100个数据分成①~⑧组,如下表所示:
那么第④组的频率为( )
| 组号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ |
| 频数 | 4 | 8 | 12 |  | 24 | 18 | 7 | 3 |
| A、24 | B、26 |
| C、0.24 | D、0.26 |
 如图,A、B、C是⊙O上的点,∠ACB=32°,则∠AOB等于( )
如图,A、B、C是⊙O上的点,∠ACB=32°,则∠AOB等于( )| A、16° | B、64° |
| C、148° | D、32° |
下列各式:y=2x2-3xz+5; y=3-2x+5x2; y=x2+2x-3; y=ax2+bx+c; y=(2x-3)(3x-2)-6x2; y=(m2+1)x2+3x-4; y=m2x2+4x-3. 是二次函数的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
各式中,分式的个数有( )
x+
y,
,
,-4xy,
,
.
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| xy |
| 1 |
| 5+a |
| x |
| x2 |
| x |
| π |
| A、1个 | B、2个 | C、3个 | D、4个 |
 同一规格的小正方体叠放成一堆,能否把这堆小正方体重新叠放成一个大正方体?若能,求叠成的大正方体的棱长与小正方体的棱长的比;若不能,请说明理由.
同一规格的小正方体叠放成一堆,能否把这堆小正方体重新叠放成一个大正方体?若能,求叠成的大正方体的棱长与小正方体的棱长的比;若不能,请说明理由.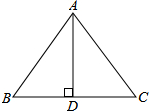 如图,在等腰△ABC中,AD是底边BC上的高,AB=AC=5,BC=6,P是线段AD上一个动点,记AP长为x,当A在以P为圆心,PB为半径的圆的外部时,求x的取值范围.
如图,在等腰△ABC中,AD是底边BC上的高,AB=AC=5,BC=6,P是线段AD上一个动点,记AP长为x,当A在以P为圆心,PB为半径的圆的外部时,求x的取值范围.