题目内容
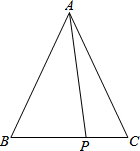 如图,在△ABC中,AB=AC=5,P是BC边上除B、C点外的任意一点,则代数式AP2+PB•PC等于( )
如图,在△ABC中,AB=AC=5,P是BC边上除B、C点外的任意一点,则代数式AP2+PB•PC等于( )| A、25 | B、15 | C、20 | D、30 |
考点:勾股定理,等腰三角形的性质
专题:计算题
分析:首先过点A作AD⊥BC于D,可得∠ADP=∠ADB=90°,又由AB=AC,根据三线合一的性质,可得BD=CD,由勾股定理可得PA2=PD2+AD2,AD2+BD2=AB2,然后由AP2+PB•PC=AP2+(BD+PD)(CD-PD),即可求得答案.
解答: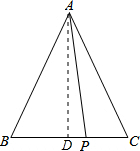 解:过点A作AD⊥BC于D,
解:过点A作AD⊥BC于D,
∵AB=AC=5,∠ADP=∠ADB=90°,
∴BD=CD,根据勾股定理得:PA2=PD2+AD2,AD2+BD2=AB2,
∴AP2+PB•PC=AP2+(BD+PD)(CD-PD)=AP2+(BD+PD)(BD-PD)=AP2+BD2-PD2=AP2-PD2+BD2=AD2+BD2=AB2=25.
故选A
 解:过点A作AD⊥BC于D,
解:过点A作AD⊥BC于D,∵AB=AC=5,∠ADP=∠ADB=90°,
∴BD=CD,根据勾股定理得:PA2=PD2+AD2,AD2+BD2=AB2,
∴AP2+PB•PC=AP2+(BD+PD)(CD-PD)=AP2+(BD+PD)(BD-PD)=AP2+BD2-PD2=AP2-PD2+BD2=AD2+BD2=AB2=25.
故选A
点评:此题考查了勾股定理,以及等腰三角形的性质,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2014年5月21日,中国石油天然气集团公司与俄罗斯天然气工业股份公司在上海签署了《中国东线供气购销合同》,这份有效期为30年的合同规定,从2018年开始供气,每年的天然气供应量为380亿立方米.380亿立方米用科学记数法表示为( )
| A、3.8×1010 |
| B、3.8×109 |
| C、3.8×108 |
| D、3.8×1011 |
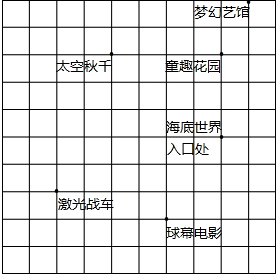 如图是“欢欢游乐城”的平面示意图,如果用(8,5)表示入口处的位置,那么(8,8)表示的位置是( )
如图是“欢欢游乐城”的平面示意图,如果用(8,5)表示入口处的位置,那么(8,8)表示的位置是( )| A、太空秋千 | B、梦幻艺馆 |
| C、童趣花园 | D、球幕电影 |
有一个底面为正三角形的直三棱柱,三视图如图所示,则这个直棱柱的侧面积为( )


| A、24 | ||
B、8
| ||
C、12
| ||
D、24+8
|
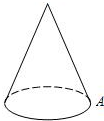 如图,地面半径为1,母线长为4的圆锥A处有一只蚂蚁,它绕这个圆锥侧面爬行一圈后回到A处,则蚂蚁所走最短路线长为( )
如图,地面半径为1,母线长为4的圆锥A处有一只蚂蚁,它绕这个圆锥侧面爬行一圈后回到A处,则蚂蚁所走最短路线长为( )| A、2 | ||
B、4
| ||
C、4
| ||
| D、4 |
 求出图中x的度数:x=
求出图中x的度数:x= 同一规格的小正方体叠放成一堆,能否把这堆小正方体重新叠放成一个大正方体?若能,求叠成的大正方体的棱长与小正方体的棱长的比;若不能,请说明理由.
同一规格的小正方体叠放成一堆,能否把这堆小正方体重新叠放成一个大正方体?若能,求叠成的大正方体的棱长与小正方体的棱长的比;若不能,请说明理由.