题目内容
如图,直线y=mx与双曲线y= 相交于A,B两点,A点坐标为(1,2).
相交于A,B两点,A点坐标为(1,2).

(1)求反比例函数的解析式;
(2)根据函数图像直接写出当mx> 时,x的取值范围;
时,x的取值范围;
(3)计算线段AB的长.
(1)y= .(2)-1<x<0或x>1;(3)2
.(2)-1<x<0或x>1;(3)2 .
.
【解析】
试题分析:(1)把A的坐标代入反比例函数的解析式即可求出答案;
(2)求出直线的解析式,解组成的方程组求出B的坐标,根据A、B的坐标结合图象即可得出答案;
(3)根据A、B的坐标.利用勾股定理分别求出OA、OB,即可得出答案.
试题解析:(1)把A(1,2)代入y= 中,2=
中,2= ,k=2
,k=2
反比例函数表达式为y= .
.
由图像知点A、点B关于原点对称,点B坐标为(-1,-2),所以当-1<x<0或x>1时,mx>
过点A作AC⊥x轴于点C,由A(1,2)得OC=1,AC=2,根据勾股定理OA= ,
,
所以AB=2OA=2 .
.
 [
[
考点:反比例函数与一次函数的交点问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 经过点A和C.
经过点A和C.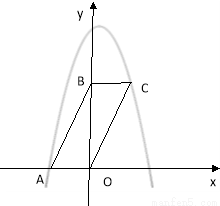
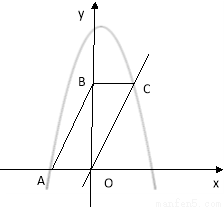
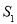 ,右侧部分图形的面积记为
,右侧部分图形的面积记为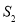 ,求
,求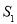 与
与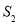 的比.
的比. ),将直线OC沿x轴平移到
),将直线OC沿x轴平移到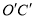 ,点D关于直线
,点D关于直线 的对称点记为
的对称点记为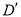 ,当点
,当点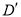 正好在抛物线上时,求出此时点
正好在抛物线上时,求出此时点 坐标并直接写出直线
坐标并直接写出直线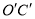 的函数解析式.
的函数解析式.
 米 C.
米 C. 米 D.50米
米 D.50米 D.
D.
 (k≠0)的图象经过点(2,﹣1),则k的值为 .
(k≠0)的图象经过点(2,﹣1),则k的值为 .