题目内容
(14分)如图,平行四边形ABCD在平面直角坐标系中,点A的坐标为(-2,0),点B的坐标为(0,4),抛物线 经过点A和C.
经过点A和C.
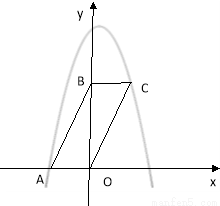
(1)求抛物线的解析式.
(2)该抛物线的对称轴将平行四边形ABCO分成两部分,对称轴左侧部分的图形面积记为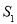 ,右侧部分图形的面积记为
,右侧部分图形的面积记为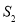 ,求
,求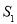 与
与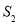 的比.
的比.
(3)在y轴上取一点D,坐标是(0, ),将直线OC沿x轴平移到
),将直线OC沿x轴平移到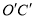 ,点D关于直线
,点D关于直线 的对称点记为
的对称点记为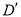 ,当点
,当点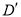 正好在抛物线上时,求出此时点
正好在抛物线上时,求出此时点 坐标并直接写出直线
坐标并直接写出直线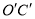 的函数解析式.
的函数解析式.
(1)  ;(2) S1:S2=23:9;(3) 点D’坐标为(-1,4)或(
;(2) S1:S2=23:9;(3) 点D’坐标为(-1,4)或( ,
, );
); 或
或 .
.
【解析】
试题分析:(1) A(-2,0),C(2,4),将其代入抛物线 ,求得解析式;
,求得解析式;
(2)通过证明CEF∽AOB,得到EF=3,应用三角形面积公式求得 与
与 的面积,进而求得
的面积,进而求得 与
与 的比;
的比;
(3)由ABO∽DMO,求得OM=7,用待定系数法求得直线DM的解析式,与抛物线解析式联立方程组求解,得到点 的坐标,得到直线
的坐标,得到直线 的解析式.
的解析式.
试题解析:【解析】
(1)∵四边形ABCO为平行四边形,∴BC∥AO,且BC=AO,
由题意知,A(-2,0),C(2,4),将其代入抛物线 中,有
中,有
 ,解得
,解得 ,
,
∴抛物线解析式为 ;
;
由(1)知,抛物线对称轴为直线 ,
,
设它交BC于点E,交OC于点F,则BE= ,CE=
,CE= .
.
又∵∠A=∠C,∴CEF∽AOB,∴ ,∴EF=3,
,∴EF=3,
∴ ,
,
又∵S□ABCD=2×4=8,∴ ,∴S1:S2=23:9.
,∴S1:S2=23:9.

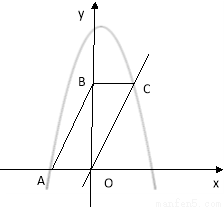
如图,设过DD’的直线交x轴于点M,交OC于点P,
∵DM⊥OC,∴∠DOP=∠DMO,
∵AB∥OC,∴∠DOC=∠ABO,∴ABO∽DMO,∴ ,∴OM=7,
,∴OM=7,
设直线DM的解析式为 ,将点D(0,
,将点D(0, ),M(7,0)代入,得
),M(7,0)代入,得
 ,解得
,解得 ,
,
∴直线DM的解析式为 ,
,
由题意得 ,解得
,解得 ,
, ,
,
∴点D’坐标为(-1,4)或( ,
, ).
).
直线O’C’的解析式为:
 (如图1)或
(如图1)或 (如图2).
(如图2).

考点:待定系数法求函数解析式;求图象的交点坐标;相似三角形的判定和性质.



 D.
D.
 向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( ) B.
B.
 D.
D.
 B.
B. C.
C. D.
D.
 +(π﹣2)0﹣(
+(π﹣2)0﹣( )﹣1= .
)﹣1= . 相交于A,B两点,A点坐标为(1,2).
相交于A,B两点,A点坐标为(1,2).
 B.
B. C.
C. D.
D.